题目内容
四边形ABCD为矩形,G是BC上的任意一点,DE⊥AG于点E.

(1)如图1,若AB=BC,BF∥DE,且交AG于点F,求证:AF-BF=EF;
(2)如图2,在(1)条件下,AG= BG,求
BG,求 ;
;
(3)如图3,连EC,若CG=CD,DE=2,GE=1,则CE= 。(直接写出结果)
(1)证明见解析;(2)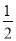 ;(3)
;(3)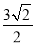 .
.
【解析】
试题分析:(1)利用△AED≌△BFA求得AE=BF,再利用线段关系求出AF-BF=EF.
(2)延长AG与DC交于点F,设BG=t先求出AB,再利用△ABG≌△FCG及直角三角形斜边上的中点,求出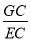 ;
;
(3)连接DG,作EM⊥BC于M点,利用直角三角形求出DG,CD的长,再利用ABG∽△DEA,求出AD,再运用△EMG∽△DEA求出EM和MG,再运用勾股定理即可求出CE的长.
试题解析:(1)∵ 四边形ABCD为正方形,
∴AD=AB,∠BAD=90°,
又DE⊥AG,BF∥DE,
∴∠AED=∠AFB=90°,
∵∠BAF+∠DAE=90°,∠BAE+∠ABF=90°,
∴∠DAE=∠ABF,
在△AED和△BFA中,

∴△AED≌△BFA(AAS),
∴AE=BF,
∴AF-BF=EF,
(2)如图2,延长AG与DC交于点F,
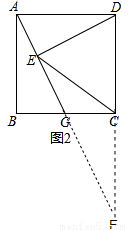
∵AG=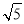 BG,设BG=t,则AG=
BG,设BG=t,则AG=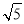 t,
t,
在Rt△ABG中,AB=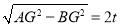 ,
,
∴G为BC的中点,
在△ABG和△FCG中,

∴△ABG≌△FCG(AAS),
∴AB=FC=CD,
又∵DE⊥AG,
在Rt△DEF中,C为斜边DF的中点,
∴EC=CD=CF,
∴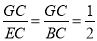 .
.
(3)如图3,连接DG,作EM⊥BC于M点,
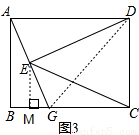
∵DE⊥AG,DE=2,GE=1,
∴在RT△DEG中,DG=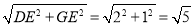 ,
,
∵CG=CD,
∴在Rt△DCG中,∠CDG=∠CGD=45°,
∴CD=CG=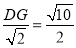 ,
,
∵∠BAG+∠GAD=90°,∠EDA+∠GAD=90°,
∴∠BAG=∠EDA,
∵∠ABG=∠DEA=90°,
∴△ABG∽△DEA,
∴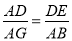 ,
,
设AD=x,则AE=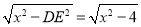 ,AG=
,AG=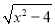 +1,
+1,
∴ ,
,
解得x1=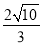 ,x2=
,x2=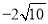 (舍去)
(舍去)
∴AE=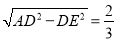 ,
,
又∵∠BAG=∠MEG,
∴∠EDA=∠MEG,
∴△EMG∽△DEA
∴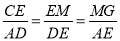 ,即
,即
解得EM= ,MG=
,MG=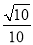 ,
,
∴CM=CG+MG=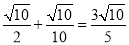 ,
,
∴CE=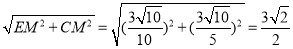 .
.
考点:四边形综合题.

