题目内容
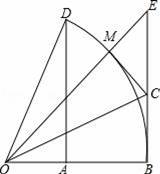
如图,△ABC中,AB=AC,AD⊥BC,CE⊥AB,AE=CE.求证:
(1)△AEF≌△CEB;
(2)AF=2CD.


【考点】全等三角形的判定与性质;等腰三角形的性质.
【专题】证明题.
【分析】(1)由AD⊥BC,CE⊥AB,易得∠AFE=∠B,利用全等三角形的判定得△AEF≌△CEB;
(2)由全等三角形的性质得AF=BC,由等腰三角形的性质“三线合一”得BC=2CD,等量代换得出结论.
【解答】证明:(1)∵AD⊥BC,CE⊥AB,
∴∠BCE+∠CFD=90°,∠BCE+∠B=90°,
∴∠CFD=∠B,
∵∠CFD=∠AFE,
∴∠AFE=∠B
在△AEF与△CEB中,
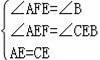
 ,
,
∴△AEF≌△CEB(AAS);
(2)∵AB=AC,AD⊥BC,
∴BC=2CD,
∵△AEF≌△CEB,
∴AF=BC,
∴AF=2CD.
【点评】本题主要考查了全等三角形性质与判定,等腰三角形的性质,运用等腰三角形的性质是解答此题的关键.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
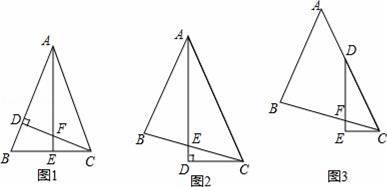


 ∠BAC,DE⊥CE,垂足为E,DE与BC交于点F.求证:DF=2CE.
∠BAC,DE⊥CE,垂足为E,DE与BC交于点F.求证:DF=2CE. >
>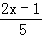 的下列过程中错误的是( )
的下列过程中错误的是( )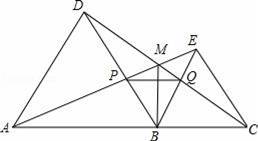


 =
=
 ﹣
﹣
 .
.
 B.
B.
 C.
C.
 D.
D.

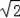
 ,若直线l满足:(1)点D到直线l的距离为1,(2)A、C两点到直线l的距离相等,则符合题意的直线l的条数为( )
,若直线l满足:(1)点D到直线l的距离为1,(2)A、C两点到直线l的距离相等,则符合题意的直线l的条数为( )

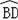
 度数为60°,∠BOE=45°,DA⊥OB,EB⊥OB.
度数为60°,∠BOE=45°,DA⊥OB,EB⊥OB.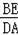
 的值;
的值;