题目内容
如图,DE是三角形ABC的边AB的垂直平分线,分别交AB、BC于D、E,AE平分∠BAC,若∠B=30度,则∠C=__________度.

90度.
【考点】线段垂直平分线的性质;三角形内角和定理.
【分析】利用线段垂直平分线的性质得∠B=∠EAB=30°,再利用角平分线的性质得解BAC的度数,根据三角形的内角和是180度即可求出角C的度数.
【解答】解:DE是三角形ABC的边AB的垂直平分线
∴AE=BE
∴∠B=∠EAB=30°
∵AE平分∠BAC
∴∠BAC=2×30°=60°
∴∠C=180°﹣60°﹣30°,
∴∠C=90°,
故填90.
【点评】本题主要考查了线段垂直平分线的性质和三角形的内角和为180度;找着角的关系利用内角和求角度是常用方法之一,要熟练掌握.

练习册系列答案
相关题目


 C.12 D.
C.12 D.
 的解集是x≥2,则( )
的解集是x≥2,则( ) +
+ =3.
=3. 图象必过原点
图象必过原点
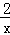 ,下列说法不正确的是( )
,下列说法不正确的是( )