题目内容
16．
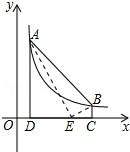如图，点A（m，6），B（n，1）在反比例函数图象上，AD⊥x轴于点D，BC⊥x轴于点C，DC=5．线段DC上有一点E，当△ABE的面积等于5时，点E的坐标为（5，0）．
分析 用待定系数法求得m，n的值，从而得出k，设E（x，0），则DE=x-1，CE=6-x，根据S△ABE=S四边形ABCD-S△ADE-S△BCE，得出x的值，即可得出点E坐标．
解答 解：由题意得：$\left\{\begin{array}{l}{6m=n}\\{m+5=n}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{m=1}\\{n=6}\end{array}\right.$，
∴A（1，6），B（6，1），
设反比例函数解析式为y=$\frac{k}{x}$，将A（1，6）代入得：k=6，
则反比例解析式为y=$\frac{6}{x}$；
设E（x，0），则DE=x-1，CE=6-x，
∵AD⊥x轴，BC⊥x轴，
∴∠ADE=∠BCE=90°，
连接AE，BE，则S△ABE=S四边形ABCD-S△ADE-S△BCE
=$\frac{1}{2}$（BC+AD）•DC-$\frac{1}{2}$DE•AD-$\frac{1}{2}$CE•BC
=$\frac{1}{2}$×（1+6）×5-$\frac{1}{2}$（x-1）×6-$\frac{1}{2}$（6-x）×1
=$\frac{35}{2}$-$\frac{5}{2}$x=5，
解得：x=5，
则E（5，0）．
点评 本题考查了反比例函数的系数k的几何意义，通过作辅助线，将图形分割，寻找全等三角形，利用边的关系设双曲线上点的坐标是解题关键．
练习册系列答案
寒假大串联黄山书社系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
4．
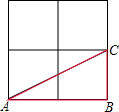如图所示，△ABC是在2×2的正方形网格中以格点为顶点的三角形，那么图中与△ABC成轴对称且也以格点为顶点的三角形共有（ ）
如图所示，△ABC是在2×2的正方形网格中以格点为顶点的三角形，那么图中与△ABC成轴对称且也以格点为顶点的三角形共有（ ）| A． | 3个 | B． | 4个 | C． | 5个 | D． | 6个 |
11．方程x2=2x的解是（ ）
| A． | x=2 | B． | x1=2，x2=0 | C． | x1=$\sqrt{2}$，x2=0 | D． | x=0 |
1．某公司准备投资开发A、B两种新产品，信息部通过市场调研得到两条信息：
信息一：如果投资A种产品，所获利润yA（万元）与投资金额x（万元）之间满足正比例函数关系：y=kx；
信息二：如果投资B种产品，所获利润yB（万元）与投资金额x（万元）之间满足二次函数关系：yB=ax2+bx．
根据公司信息部报告，yA、yB（万元）与投资金额x（万元）的部分对应值如上表所示：
（1）填空：yA=0.6x； yB=-0.2x2+2.6x；
（2）如果公司准备投资15万元同时开发A、B两种新产品，设公司所获得的总利润为W（万元），B种产品的投资金额为x（万元），试求出W与x之间的函数关系式；
（3）请你设计一个在（2）中公司能获得最大总利润的投资方案．
| x（万元） | 1 | 2 |
| yA（万元） | 0.6 | 1.2 |
| yB（万元） | 2.4 | 4.4 |
信息二：如果投资B种产品，所获利润yB（万元）与投资金额x（万元）之间满足二次函数关系：yB=ax2+bx．
根据公司信息部报告，yA、yB（万元）与投资金额x（万元）的部分对应值如上表所示：
（1）填空：yA=0.6x； yB=-0.2x2+2.6x；
（2）如果公司准备投资15万元同时开发A、B两种新产品，设公司所获得的总利润为W（万元），B种产品的投资金额为x（万元），试求出W与x之间的函数关系式；
（3）请你设计一个在（2）中公司能获得最大总利润的投资方案．
在三角形ABC中，∠B=90°，D在AC边上，DF⊥BC于F，DE⊥AB于E，则线段AB与DF平行吗？BC与DE平行吗？为什么．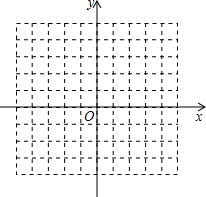
如图，已知A（-3，-3），B（-2，-1），C（-1，-3）是直角坐标平面上三点．