题目内容
用反证法证明“两条直线相交，只能有一个交点”，应假设 ．
考点：反证法
专题：
分析：反证法的步骤中，第一步是假设结论不成立，反面成立，可据此进行解答．
解答：解：用反证法证明“两条直线相交，只能有一个交点”，应假设两条直线相交，有两个或两个以上交点，
故答案为：两条直线相交，有两个或两个以上交点．
故答案为：两条直线相交，有两个或两个以上交点．
点评：本题结合直线的位置关系考查反证法，解此题关键要懂得反证法的意义及步骤．在假设结论不成立时要注意考虑结论的反面所有可能的情况，如果只有一种，那么否定一种就可以了，如果有多种情况，则必须一一否定．
练习册系列答案
相关题目
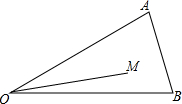如图，M是△AOB内一点，已知∠AOB=30°，OM=2，试在OA上确定一点E，在OB上确定一点F，使△MEF的周长最小，并求出△MEF周长的最小值．
如图长方形MNPQ是菜市民健身广场的平面示意图，它是由6个正方形拼成的长方形，中间最小的正方形A的边长是1，观察图形特点可知长方形相对的两边是相等的（如图中MN=PQ）．正方形四边相等．请根据这个等量关系，试计算长方形MNPQ的面积，结果为
将正整数按如图所示的规律排列下去，若用整数对（m，n）表示第m排，从左到右第n个数，如（4，3）表示整数9，则（8，4）表示整数是已知点A（1，y1）、B（2，y2）、C（-3，y3）都在正比例函数y=-2x的图象上，则y1、y2、y3的大小关系是（ ）
| A、y3＜y1＜y2 |
| B、y1＜y2＜y3 |
| C、y2＜y1＜y3 |
| D、y3＜y2＜y1 |
