题目内容
17.一个大的等腰三角形能被分割为两个小等腰三角形,则该大等腰三角形顶角的度数是108°或90°或36°或$\frac{180°}{7}$.分析 因为题中没有指明这个等腰三角形是什么形状,故应该分四种情况进行分析,从而得到答案.
解答  解:(1)如图1,△ABC中,AB=AC,BD=AD,AC=CD,求∠BAC的度数.
解:(1)如图1,△ABC中,AB=AC,BD=AD,AC=CD,求∠BAC的度数.
∵AB=AC,BD=AD,AC=CD,
∴∠B=∠C=∠BAD,∠CDA=∠CAD,
∵∠CDA=2∠B,
∴∠CAB=3∠B,
∵∠BAC+∠B+∠C=180°,
∴5∠B=180°,
∴∠B=36°,
∴∠BAC=108°. (2)如图2,△ABC中,AB=AC,AD=BD=CD,求∠BAC的度数.
(2)如图2,△ABC中,AB=AC,AD=BD=CD,求∠BAC的度数.
∵AB=AC,AD=BD=CD,
∴∠B=∠C=∠DAC=∠DAB
∴∠BAC=2∠B
∵∠BAC+∠B+∠C=180°,
∴4∠B=180°,
∴∠B=45°,
∴∠BAC=90°. (3)如图3,△ABC中,AB=AC,BD=AD=BC,求∠BAC的度数.
(3)如图3,△ABC中,AB=AC,BD=AD=BC,求∠BAC的度数.
∵AB=AC,BD=AD=BC,
∴∠B=∠C,∠A=∠ABD,∠BDC=∠C
∵∠BDC=2∠A,
∴∠C=2∠A=∠B,
∵∠A+∠ABC+∠C=180°,
∴5∠A=180°,
∴∠A=36°. (4)如图4,△ABC中,AB=AC,BD=AD,CD=BC,求∠BAC的度数.
(4)如图4,△ABC中,AB=AC,BD=AD,CD=BC,求∠BAC的度数.
假设∠A=x,AD=BD,
∴∠DBA=x,
∵AB=AC,
∴∠DBC=$\frac{180°-x}{2}$-x,
CD=BC,
∴∠BDC=2x=∠DBC=$\frac{180°-x}{2}$-x,
解得:x=$\frac{180°}{7}$.
故答案为:108°或90°或36°或$\frac{180°}{7}$.
点评 本题考查了等腰三角形的性质,等腰直角三角形的性质,熟记等腰直角三角形的性质是解题的关键.

练习册系列答案
 同步奥数系列答案
同步奥数系列答案
相关题目
8.若不等式组$\left\{\begin{array}{l}{1+x<a}\\{\frac{x+1}{2}≤\frac{x+2}{3}-1}\end{array}\right.$ 的解是x<a-1,则实数a的取值范围是( )
| A. | a≤-6 | B. | a≤-5 | C. | a≤-4 | D. | a<-4 |
12.下列运算正确的是( )
| A. | 3a+2a=5a2 | B. | a2•a3=a6 | C. | (a+b)(a-b)=a2-b2 | D. | (a+b)2=a2+b2 |
2.在下列各几何图形中,有对称中心但没有对称轴的是( )
| A. | 圆 | B. | 正方形 | C. | 平行四边形 | D. | 等边三角形 |
9.设口袋中有5个完全相同的小球,它们的标号分别为1,2,3,4,5.现从中随机摸出(同时摸出)二个小球并记下标号,则标号之和大于5的概率是( )
| A. | $\frac{3}{10}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{7}{10}$ |
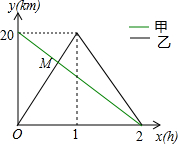 在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地;乙骑自行车从B地到A地,到达A地后立即按原路返回,如图是甲、乙两人离B地的距离y(km)与行驶时间x(h)之间的函数图象,根据图象解答以下问题:
在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地;乙骑自行车从B地到A地,到达A地后立即按原路返回,如图是甲、乙两人离B地的距离y(km)与行驶时间x(h)之间的函数图象,根据图象解答以下问题: