题目内容
16.在?ABCD中,BC=24,AB=18,∠ABC和∠BCD的平分线交AD于点E、F,求EF的长.分析 求出AB=CD,AD∥BC,根据平行线性质和角平分线性质求出∠ABE=∠AEB,推出AB=AE,同理求出DF=CD,求出AE=DF,进而得出EF的长.
解答 解:∵四边形ABCD是平行四边形,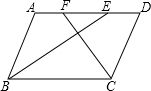
∴AB=CD,AD∥BC,
∴∠AEB=∠EBC,
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∴∠ABE=∠AEB,
∴AB=AE,
同理DF=CD,
∴AE=DF,
即AE-EF=DF-EF,
∴AF=DE,
∵AB=18,BC=24,
∴DE=AD-AE=24-18=6,
EF=DF-DE=18-6=12.
点评 本题考查了平行四边形性质,平行线性质,矩形的判定,角平分线性质,等腰三角形的性质和判定等知识点的应用,能综合运用性质进行推理是解此题的关键,题目比较典型,难度适中.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.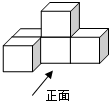 如图,一个几何体由5个大小相同、棱长为1的正方体搭成,下列关于这个几何体的说法错误的是( )
如图,一个几何体由5个大小相同、棱长为1的正方体搭成,下列关于这个几何体的说法错误的是( )
 如图,一个几何体由5个大小相同、棱长为1的正方体搭成,下列关于这个几何体的说法错误的是( )
如图,一个几何体由5个大小相同、棱长为1的正方体搭成,下列关于这个几何体的说法错误的是( )| A. | 主视图的面积为4 | B. | 左视图的面积为3 | ||
| C. | 俯视图的面积为4 | D. | 搭成的几何体的表面积是20 |
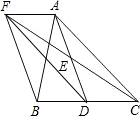 如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行弦交CE的延长线于点F,且AF=BD,连接BF,FD.
如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行弦交CE的延长线于点F,且AF=BD,连接BF,FD.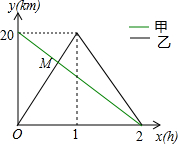 在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地;乙骑自行车从B地到A地,到达A地后立即按原路返回,如图是甲、乙两人离B地的距离y(km)与行驶时间x(h)之间的函数图象,根据图象解答以下问题:
在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地;乙骑自行车从B地到A地,到达A地后立即按原路返回,如图是甲、乙两人离B地的距离y(km)与行驶时间x(h)之间的函数图象,根据图象解答以下问题: