题目内容

14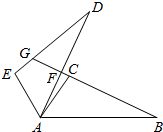．如图，△ABC≌△ADE，且∠CAD=10°，∠D=25°，∠EAB=120°．求∠DFB和∠DGB的度数．

分析 根据全等三角形的性质得到∠EAD=∠CAB，求出∠E，根据三角形的外角的性质解答即可．

解答 解：∵△ABC≌△ADE，
∴∠EAD=∠CAB=$\frac{1}{2}$（∠EAB-∠CAD）=55°，
∴∠E=180°-∠EAD-∠D=100°，
∵△ABC≌△ADE，
∴∠ACB=∠E=100°，
∴∠AFB=∠ACB-∠CAD=90°，
∴∠DFB=90°，
∴∠DGB=90°-∠D=65°．

点评 本题考查的是全等三角形的性质、三角形的外角的性质，掌握全等三角形的对应边相等、全等三角形的对应角相等是解题的关键．

练习册系列答案
相关题目
4．计算：
（1）（$\sqrt{3}$）2+|1-$\sqrt{3}$|+（$\frac{1}{2}$）0
（2）如图，a，b，c是数轴上三个点A、B、C所对应的实数．试化简：
$\sqrt{{c}^{2}}$-|a-b|+$\root{3}{（a+b）^{3}}$-|b-c|．
5．计算
（1）（+16）-（-5）-（+6）+（-7）+10     
（2）-23÷8×（-7）-（-2）3
（3）（2x2-x）-[5x2-（3x3-x）]
（4）（$\frac{1}{2}$-$\frac{1}{3}$+$\frac{5}{6}$-$\frac{1}{12}$+$\frac{1}{4}$）×36．
2．如图，抛物线y=ax2+bx+c（a≠0）的顶点坐标为（2，-1），图象与y轴交于点C（0，3），与x轴交于A、B两点．
（1）求抛物线的解析式；
（2）设抛物线对称轴与直线BC交于点D，连接AC、AD，求△ACD的面积；
（3）点E为直线BC上的任意一点，过点E作x轴的垂线与抛物线交于点F，问是否存在点E使△DEF为直角三角形？若存在，求出点E坐标，若不存在，请说明理由．
9．若|x|=3，|y|=4，且|x-y|=y-x，则xy的值为（　　）
A．-1B．-12C．12D．12或-12
19．已知a、b、c都是有理数，且满足$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$=1，则$\frac{abc}{|abc|}$=（　　）
A．1B．-1C．±1D．2
6．（1）计算$\sqrt{24}$÷$\sqrt{3}$-$\frac{6}{\sqrt{2}}$+$\sqrt{32}$
（2）计算（$\sqrt{3}$+$\sqrt{2}$）（$\sqrt{3}$-$\sqrt{2}$）
3．计算：
（1）（$\frac{1}{9}$-$\frac{2}{3}$+$\frac{3}{5}$）×45            
（2）-24-2×（-3）+|2-5|-（-1）2013．
4．如图所示，在△ABC中，∠ABC=60°，AD、CE分别平分∠BAC，∠ACB，AD、CE相交于点O，下列结论不一定正确的是（　　）
A．∠AOC=120°B．OE=OD
C．BE=BDD．S△AEO+S△CDO=S△ACO

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网