题目内容
如图1,在面积为3的正方形ABCD中,E、F分别是BC和CD边上的两点,AE⊥BF于点G,且BE=1,∠BAE=30°.

(1)求证:△ABE≌△BCF;
(2)求出△ABE和△BCF重叠部分(即△BEG)的面积;
(3)现将△ABE绕点A逆时针方向旋转到△AB'E'(如图2),使点E落在CD边上的点E'处,问△ABE在旋转前后与△BCF重叠部分的面积是否发生了变化?请说明理由.
(1)证明见解析;
(2) ;
;
(3)没有变化,理由见解析.
【解析】
试题分析:(1)要证△ABE≌△BCF,已知条件是AB=BC ,∠ABE=∠BCF=90°,只需要再有一条边或一个角对应相等即可,而通过已知条件可以得到∠BAE=∠CBF,利用ASA即可证全等了;
(2)由(1)△ABE≌△BCF,可得∠FBC=∠BAE=30°,又BE=1,∠BGE=90°,从而可得GE= ,利用勾股定理可得GB的长,从而可得△BEG)的面积;
,利用勾股定理可得GB的长,从而可得△BEG)的面积;
(3)由已知条件可得Rt△ABE≌Rt△AB'E'≌Rt△AD E', △BAG≌△HAG,从而可得S四边形B’E’HG=S△AB’E’-S三角形AGH=S△ABE-S△ABG=S△BEG,即重叠部分的面积没有变化.
试题解析:⑴∵正方形ABCD中,∠ABE=∠BCF=90°,AB=BC,
∴∠ABF+∠CBF=900,∵AE⊥BF, ∴∠ABF+∠BAE=900,
∴∠BAE=∠CBF, ∴△ABE≌△BCF.
⑵∵△ABE≌△BCF,∴∠FBC=∠BAE=30°,∵BE=1,∠BGE=90°,∴GE= ,∴GB=
,∴GB= =
=
∴S△BGE= ×
× ×
× =
= .
.
(3)没有变化,易证Rt△ABE≌Rt△AB'E'≌Rt△AD E', △BAG≌△HAG,
∴S四边形B’E’HG=S△AB’E’-S三角形AGH=S△ABE-S△ABG=S△BEG
∴△ABE在旋转前后与△BCF重叠部分的面积没有变化.
考点:1、正方形的性质;2、三角形全等的判定与性质;3、旋转的性质;4、勾股定理.

 名校课堂系列答案
名校课堂系列答案 ,其中x=
,其中x= .
. 中,
中, ,如果
,如果 ,
, ,那么
,那么 ;
; ∥
∥ ∥
∥ ,
, ,
, ,那么
,那么 的长等于( )
的长等于( )
 ; D.
; D.  ;
;


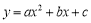
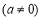 的对称轴为直线
的对称轴为直线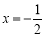 .下列结论中,正确的是( )
.下列结论中,正确的是( )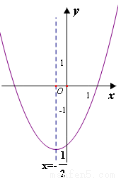
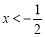 时, y随x的增大而增大
时, y随x的增大而增大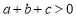
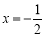 时,y的最小值是
时,y的最小值是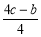
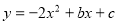 的图像经过点A(0,4)和B(1,-2).
的图像经过点A(0,4)和B(1,-2). 的长为( )
的长为( )