题目内容
6.设a+b>c>0,且|a-b|<c,那么关于x的一元二次方程a2x2+(b2+a2-c2)x+b2=0的根的情况( )| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 没有实数根 | D. | 根的情况无法判断 |
分析 由根的判别式得出△=(b2+a2-c2)2-4a2b2=(a+b+c)(a+b-c)(a-b+c)(a-b-c),再根据a+b>c>0,且|a-b|<c得a+b+c>0,a+b-c>0,-c<a-b<c,继而知a-b+c>0,a-b-c<0,从而判断出△<0可得答案.
解答 解:∵△=(b2+a2-c2)2-4a2b2
=(b2+a2-c2+2ab)(b2+a2-c2-2ab)
=[(a+b)2-c2][(a-b)2-c2]
=(a+b+c)(a+b-c)(a-b+c)(a-b-c),
∵a+b>c>0,且|a-b|<c,
∴a+b+c>0,a+b-c>0,-c<a-b<c,
∴a-b+c>0,a-b-c<0,
则△=(a+b+c)(a+b-c)(a-b+c)(a-b-c)<0,
∴此方程无实数根,
故选:C.
点评 本题主要考查一元二次方程根的判别式,一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:
①当△>0时,方程有两个不相等的两个实数根;②当△=0时,方程有两个相等的两个实数根;③当△<0时,方程无实数根.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.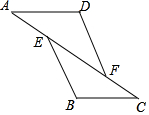 如图,已知AE=CF,∠A=∠C,那么添加下列一个条件后,仍无法判定△ADF≌△CBE的是( )
如图,已知AE=CF,∠A=∠C,那么添加下列一个条件后,仍无法判定△ADF≌△CBE的是( )
 如图,已知AE=CF,∠A=∠C,那么添加下列一个条件后,仍无法判定△ADF≌△CBE的是( )
如图,已知AE=CF,∠A=∠C,那么添加下列一个条件后,仍无法判定△ADF≌△CBE的是( )| A. | ∠D=∠B | B. | BE=DF | C. | AD=CB | D. | BE∥DF |
14. 如图,若有理数a、b在数轴上的对应点的位置如图所示,则下列各式错误的是( )
如图,若有理数a、b在数轴上的对应点的位置如图所示,则下列各式错误的是( )
 如图,若有理数a、b在数轴上的对应点的位置如图所示,则下列各式错误的是( )
如图,若有理数a、b在数轴上的对应点的位置如图所示,则下列各式错误的是( )| A. | $\frac{|a|}{a}$+$\frac{|b|}{b}$=0 | B. | a+b<0 | C. | |a+b|-a=b | D. | -b<a<-a<b |
1. 如图,点P位于点O的( )
如图,点P位于点O的( )
 如图,点P位于点O的( )
如图,点P位于点O的( )| A. | 南偏西32° | B. | 北偏东32° | C. | 南偏东58° | D. | 北偏西58° |
18. 如图,把“QQ”笑脸放在直角坐标系中,已知右眼A的坐标是(-2,3),嘴唇C点的坐标为(-1,1),则此“QQ”笑脸左眼B的坐标是( )
如图,把“QQ”笑脸放在直角坐标系中,已知右眼A的坐标是(-2,3),嘴唇C点的坐标为(-1,1),则此“QQ”笑脸左眼B的坐标是( )
 如图,把“QQ”笑脸放在直角坐标系中,已知右眼A的坐标是(-2,3),嘴唇C点的坐标为(-1,1),则此“QQ”笑脸左眼B的坐标是( )
如图,把“QQ”笑脸放在直角坐标系中,已知右眼A的坐标是(-2,3),嘴唇C点的坐标为(-1,1),则此“QQ”笑脸左眼B的坐标是( )| A. | (0,3) | B. | (0,1) | C. | (-1,2) | D. | (-1,3) |
16. 某课题组为了解全市九年级学生对数学知识的掌握情况,在一次数学检测中,从全市20000 名九年级考生中随机抽取部分学生的数学成绩进行调查,并将调查结果绘制成如图表:
某课题组为了解全市九年级学生对数学知识的掌握情况,在一次数学检测中,从全市20000 名九年级考生中随机抽取部分学生的数学成绩进行调查,并将调查结果绘制成如图表:
(1)表中a和b所表示的数分别为:a=40,b=0.14;
(2)请在图中补全额数分布直方图;
(3)如果把成绩在70分以上(含70分)定为合格,那么该市20000名九年级考生数学成绩为合格的学生约有多少名?
 某课题组为了解全市九年级学生对数学知识的掌握情况,在一次数学检测中,从全市20000 名九年级考生中随机抽取部分学生的数学成绩进行调查,并将调查结果绘制成如图表:
某课题组为了解全市九年级学生对数学知识的掌握情况,在一次数学检测中,从全市20000 名九年级考生中随机抽取部分学生的数学成绩进行调查,并将调查结果绘制成如图表:| 分数段 | 频数 | 频率 |
| 50≤x≤60 | 20 | 0.10 |
| 60≤x≤70 | 28 | b |
| 70≤x≤80 | 54 | 0.27 |
| 80≤x≤90 | a | 0.20 |
| 90≤x≤100 | 24 | 0.12 |
| 100≤x≤110 | 18 | 0.09 |
| 110≤x≤120 | 16 | 0.08 |
(2)请在图中补全额数分布直方图;
(3)如果把成绩在70分以上(含70分)定为合格,那么该市20000名九年级考生数学成绩为合格的学生约有多少名?
 如图,已知线段AB=8cm,延长线段AB到C,使BC=2AB,点D是AC的中点,则BD等于4cm.
如图,已知线段AB=8cm,延长线段AB到C,使BC=2AB,点D是AC的中点,则BD等于4cm. 如图,在直角△ABC中,斜边AB上的垂直平分线交直角边BC于D,交AB于E,若BC=10cm,AC=6cm,则△ADC的周长为16cm.
如图,在直角△ABC中,斜边AB上的垂直平分线交直角边BC于D,交AB于E,若BC=10cm,AC=6cm,则△ADC的周长为16cm.