题目内容
16.一个不透明的口袋中装有2个红球、1个白球、1个黑球,这些球除颜色外都相同,将球摇匀.(1)从中任意摸出1个球,恰好摸到红球的概率是$\frac{1}{2}$;
(2)先从中任意摸出1个球,再从余下的3个球中任意摸出1个球,请用列举法(画树状图或列表)求两次都摸到红球的概率.
分析 (1)根据4个小球中红球的个数,即可确定出从中任意摸出1个球,恰好摸到红球的概率;
(2)列表得出所有等可能的情况数,找出两次都摸到红球的情况数,即可求出所求的概率.
解答 解:(1)4个小球中有2个红球,
则任意摸出1个球,恰好摸到红球的概率是$\frac{1}{2}$;
故答案为:$\frac{1}{2}$;
(2)列表如下:
| 红 | 红 | 白 | 黑 | |
| 红 | --- | (红,红) | (白,红) | (黑,红) |
| 红 | (红,红) | --- | (白,红) | (黑,红) |
| 白 | (红,白) | (红,白) | --- | (黑,白) |
| 黑 | (红,黑) | (红,黑) | (白,黑) | --- |
则P(两次摸到红球)=$\frac{2}{12}$=$\frac{1}{6}$.
点评 此题考查的是用列表法或树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;解题时要注意此题是放回实验还是不放回实验.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
11.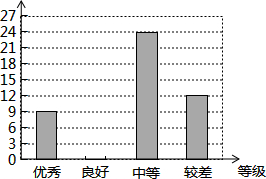 为进一步加强学习贯彻2015年新修订的《中小学生守则》,某校组织全校学生参加安溪县中小学“学守则•促文明•行规范”校园猜谜比赛,将比赛成绩分为“优秀、良好、中等、较差”四个等级.现从中随机抽取该校部分学生的比赛成绩进行统计分析,并制成了如下的统计图表:
为进一步加强学习贯彻2015年新修订的《中小学生守则》,某校组织全校学生参加安溪县中小学“学守则•促文明•行规范”校园猜谜比赛,将比赛成绩分为“优秀、良好、中等、较差”四个等级.现从中随机抽取该校部分学生的比赛成绩进行统计分析,并制成了如下的统计图表:
根据图表信息,回答下列问题:
(1)本次抽查的学生共有60名;
(2)统计表中所表示的数a=15,b=20%,并将条形统计图补充完整;
(3)已知该校共有1800名学生参加比赛,请你估计比赛成绩达到“良好”或“优秀”等级的人数约是多少?
 为进一步加强学习贯彻2015年新修订的《中小学生守则》,某校组织全校学生参加安溪县中小学“学守则•促文明•行规范”校园猜谜比赛,将比赛成绩分为“优秀、良好、中等、较差”四个等级.现从中随机抽取该校部分学生的比赛成绩进行统计分析,并制成了如下的统计图表:
为进一步加强学习贯彻2015年新修订的《中小学生守则》,某校组织全校学生参加安溪县中小学“学守则•促文明•行规范”校园猜谜比赛,将比赛成绩分为“优秀、良好、中等、较差”四个等级.现从中随机抽取该校部分学生的比赛成绩进行统计分析,并制成了如下的统计图表:| 比赛成绩等级 | 人数 | 百分比 |
| 较差 | 12 | b |
| 中等 | 24 | c |
| 良好 | a | 25% |
| 优秀 | 9 | 15% |
(1)本次抽查的学生共有60名;
(2)统计表中所表示的数a=15,b=20%,并将条形统计图补充完整;
(3)已知该校共有1800名学生参加比赛,请你估计比赛成绩达到“良好”或“优秀”等级的人数约是多少?
1.下列运算正确的是( )
| A. | (a-b)2=a2-b2 | B. | -2x2+x2=-3x2 | C. | $\sqrt{(-2)^{2}}$=-2 | D. | a2•a3=a5 |
8.下列各式正确的是( )
| A. | x2+x3=x5 | B. | x3•x2=2x5 | C. | x5÷x3=x2 | D. | (x5)2=x7 |
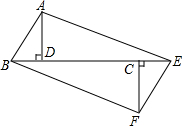 如图,已知△ABD和△CEF都是斜边为2cm的全等直角三角形,其中∠ABD=∠FEC=60°,且B、D、C、E都在同一直线上,DC=4.
如图,已知△ABD和△CEF都是斜边为2cm的全等直角三角形,其中∠ABD=∠FEC=60°,且B、D、C、E都在同一直线上,DC=4.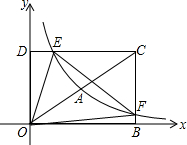 如图,在平面直角坐标系xOy中,已知四边形DOBC是矩形,且D(0,4),B(6,0).若反比例函数$y=\frac{k}{x}$(x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F.设直线EF的解析式为y=mx+n.
如图,在平面直角坐标系xOy中,已知四边形DOBC是矩形,且D(0,4),B(6,0).若反比例函数$y=\frac{k}{x}$(x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F.设直线EF的解析式为y=mx+n.