题目内容
18.如图①,在 Rt△ABC中,∠BAC=90°,AB=AC,将一块含45°的直角三角板ADE如图放置,使三角板的直角顶点与点A重合,点D在△ABC内,点E在△ABC外,连接CD,BE.(1)求证:CD=BE;
(2)当点C,D,E在同一直线上时,如图②,请问△BCE是什么三角形?请说明理由.

分析 (1)只要证明△CAD≌△BAE即可解决问题.
(2)结论:△BCE是直角三角形.利用“8字型”证明直角即可.
解答 (1)证明:∵∠CAB=∠DAE=90°,
∴∠CAD=∠BAE,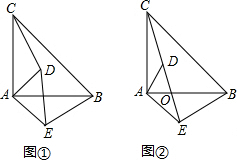
在△CAD和△BAE中,
$\left\{\begin{array}{l}{CA=AB}\\{∠CAD=∠BAE}\\{AD=AE}\end{array}\right.$,
∴△CAD≌△BAE,
∴CD=BE.
解:(2)结论:△BCE是直角三角形.
理由:如图设AB与CE交于点O.
∵△CAD≌△BAE,
∴∠OCA=∠OBE,
∵∠AOC=∠BOE,
∴∠OEB=∠OAC=90°,
∴△BCE是直角三角形.
点评 本题考查全等三角形的判定和性质、等腰直角三角形的性质等知识,解题的关键是正确寻找全等三角形解决问题,学会利用“8字型”证明直角,属于中考常考题型.

练习册系列答案
相关题目
6. 如图是一次函数y=kx+b的图象,当y<-2时,x的取值范围是( )
如图是一次函数y=kx+b的图象,当y<-2时,x的取值范围是( )
 如图是一次函数y=kx+b的图象,当y<-2时,x的取值范围是( )
如图是一次函数y=kx+b的图象,当y<-2时,x的取值范围是( )| A. | x<3 | B. | x>3 | C. | x<-1 | D. | x>-1 |
10.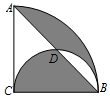 如图,在半径为2,圆心角为90°的扇形内,以BC为直径作半圆,交弦AB于点D,连接CD,则阴影部分的面积为( )
如图,在半径为2,圆心角为90°的扇形内,以BC为直径作半圆,交弦AB于点D,连接CD,则阴影部分的面积为( )
 如图,在半径为2,圆心角为90°的扇形内,以BC为直径作半圆,交弦AB于点D,连接CD,则阴影部分的面积为( )
如图,在半径为2,圆心角为90°的扇形内,以BC为直径作半圆,交弦AB于点D,连接CD,则阴影部分的面积为( )| A. | π-1 | B. | 2π-1 | C. | 2π-2 | D. | π-2 |
8.计算|-$\frac{3}{2}$|+1的结果是( )
| A. | $\frac{5}{2}$ | B. | 1 | C. | -$\frac{1}{2}$ | D. | -$\frac{1}{4}$ |