题目内容
1.已知a,b,c是△ABC的三边长,且满足关系式a3+ab2-ac2+a2b+b3-bc2=0,则△ABC的形状为直角三角形.分析 利用分组分解法提公因式法对等式进行变形,再进一步判定三角形的形状.
解答 解:∵a3+ab2-ac2+a2b+b3-bc2=0,
∴(a3+a2b)+(ab2+b3)-(bc2+ac2)=0,
a2(a+b)+b2(a+b)-c2(a+b)=0,
(a+b)(a2+b2-c2)=0,
∵a,b,c是△ABC的三边长,
∴a+b>0,
∴a2+b2=c2,
则三角形是直角三角形.
故答案为直角三角形.
点评 本题考查了分组分解法分解因式,利用因式分解最后整理成多项式的乘积等于0的形式是解题的关键.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
12.已知两个分式:A=$\frac{2}{x-3}$-$\frac{1}{x}$,B=$\frac{x+3}{{x}^{2}-3x}$,其中x≠3且x≠0,则A与B的关系是( )
| A. | 相等 | B. | 互为倒数 | C. | 互为相反数 | D. | 不能确定 |
6.下列说法中错误的是( )
| A. | 等腰三角形至少有两个角相等 | |
| B. | 等腰三角形的底角一定是锐角 | |
| C. | 等腰三角形顶角的外角是底角的2倍 | |
| D. | 等腰三角形中有一个角是45°,那它一定是等腰直角三角形 |
11.如图,将一个长为12cm,宽为6cm的矩形纸片对折两次后,沿所得矩形两邻边中点的连线(虚线)剪下,再打开,得到的菱形的面积为( )


| A. | 9cm2 | B. | 18cm2 | C. | 27cm2 | D. | 72cm2 |
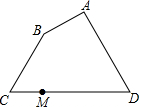 如图,
如图,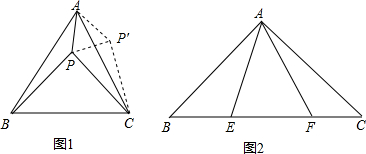
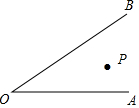 如图,点P在∠AOB内.
如图,点P在∠AOB内.