题目内容
3.(1)有一列数按一定规律排列为1,-3,5,-7、9,…,如果其中三个相邻的数之和为-201,求这三个数;(2)有一列数,按一定规律排列成1,-3,9,-27,81,-243,…,其中某三个相邻数的和是-1701,求这三个数中最小的数.
分析 (1)设中间的数为x,则另外两个数为-x-2,-x+2,让3个数相加等于-201求值即可.
(2)本题需先设出最左边的数为x,再根据数字的变化规律的出其它两数分别为-3x,9x,然后列出方程,求出x的值,即可求出结果.
解答 解:(1)设三个数中间的一个为x,依题意得:
(-x-2)+x+(-x+2)=-201,
解得:x=201,
则-x+2=-199,
-x-2=-203.
答:这三个数为-199、201、-203.
(2)由题意可得:an=(-3)an-1,
设从左到右最左边的数为x,则其它两数分别为-3x,9x,
x-3x+9x=-1701,
x=-243,
则三个数中最小的数是:-243×9=-2187.
故这三个数中最小的数-2187.
点评 此题考查了规律型:数字的变化类,用一元一次方程解决实际问题,得到数列中相邻两数的关系是解决本题的突破点.

练习册系列答案
相关题目
13.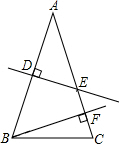 如图,已知在△ABC中,AB=AC,AB的垂直平分线DE交AC于点E,CE的垂直平分线正好经过点B,与AC相交于点F,求∠A的度数是( )
如图,已知在△ABC中,AB=AC,AB的垂直平分线DE交AC于点E,CE的垂直平分线正好经过点B,与AC相交于点F,求∠A的度数是( )
 如图,已知在△ABC中,AB=AC,AB的垂直平分线DE交AC于点E,CE的垂直平分线正好经过点B,与AC相交于点F,求∠A的度数是( )
如图,已知在△ABC中,AB=AC,AB的垂直平分线DE交AC于点E,CE的垂直平分线正好经过点B,与AC相交于点F,求∠A的度数是( )| A. | 30° | B. | 35° | C. | 45° | D. | 36° |
14.若式子$\frac{1-x}{2}$与1-$\frac{x+1}{3}$的值相等,则x=( )
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
11.-2的绝对值是( )
| A. | $\frac{1}{2}$ | B. | ±2 | C. | 2 | D. | -2 |
18.下列四组等式变形中,正确的是( )
| A. | 由5x+7=0,得5x=-7 | B. | 由2x-3=0,得2x-3+3=0 | ||
| C. | 由$\frac{x}{6}$=2,得x=$\frac{1}{3}$ | D. | 由5x=7.得x=$\frac{5}{7}$ |
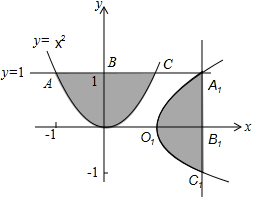 如图,把抛物线y=x2与直线y=1围成的图形OABC绕原点O顺时针旋转90°后,再沿x轴向右平移1个单位得到图形O1A1B1C1.
如图,把抛物线y=x2与直线y=1围成的图形OABC绕原点O顺时针旋转90°后,再沿x轴向右平移1个单位得到图形O1A1B1C1.