题目内容
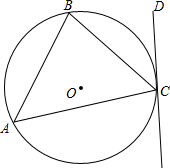如图所示，A、B、C三点都在⊙O上，直线DE过点C，∠BCD=∠BAC，求证：DE与⊙O相切．考点：切线的判定
专题：证明题
分析：过点C作直径CE，连结BE，如图，根据圆周角定理由CE为直径得∠CBE=90°，则∠E+∠BCE=90°，加上∠BCD=∠BAC，∠BAC=∠E，所以∠BCD+∠BCE=90°，然后根据切线的判定定理即可得到结论．
解答：
证明：过点C作直径CE，连结BE，如图，
∵CE为直径，
∴∠CBE=90°，
∴∠E+∠BCE=90°，
∵∠BCD=∠BAC，∠BAC=∠E，
∴∠E=∠BCD，
∴∠BCD+∠BCE=90°，
∴OC⊥CD，
∴DE与⊙O相切．
证明：过点C作直径CE，连结BE，如图，∵CE为直径，
∴∠CBE=90°，
∴∠E+∠BCE=90°，
∵∠BCD=∠BAC，∠BAC=∠E，
∴∠E=∠BCD，
∴∠BCD+∠BCE=90°，
∴OC⊥CD，
∴DE与⊙O相切．
点评：本题考查了切线的判定：经过半径的外端且垂直于这条半径的直线是圆的切线．也考查了圆周角定理．
练习册系列答案
优等生题库系列答案
相关题目
如图，ABCD为圆内正方形，AD=4，弦AE平分BC交BC于点M，则CE长为
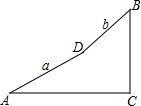如图：BC⊥AC，设AD=a，DB=b，∠A=α，∠B=β，则用含a、b、α、β的式子表示AC正确的为（ ）| A、asinα+bsinβ |
| B、asinα+bcosβ |
| C、acosα+bsinβ |
| D、acosα+bcosβ |