题目内容
如图，ABCD为圆内正方形，AD=4，弦AE平分BC交BC于点M，则CE长为考点：相似三角形的判定与性质,正方形的性质,圆周角定理
专题：常规题型
分析：根据圆周角定理和正方形的性质可以求得∠AEC=90°，AM的值，再证明△AMB∽△CME，根据相似三角形对应边比例即可解题．
解答：解：连接AC，BE，
∵四边形ABCD为圆内正方形，∴AC必过圆心O，且∠AEC=∠ABC=90°，
∵∠CME=∠AMB，
∴△AMB∽△CME，
∴
=
．
∵AM=
=2
，
∴
=
，
∴CE=
．
故答案为
．
∵四边形ABCD为圆内正方形，∴AC必过圆心O，且∠AEC=∠ABC=90°，
∵∠CME=∠AMB，
∴△AMB∽△CME，
∴
| AB |
| CE |
| AM |
| MC |
∵AM=
| AB2+BM2 |
| 5 |
∴
| 4 |
| CE |
2
| ||
| 2 |
∴CE=
4
| ||
| 5 |
故答案为
4
| ||
| 5 |
点评：本题考查了相似三角形的判定，考查了相似三角形对应边比例相等的性质．
练习册系列答案
相关题目
如图，AB是⊙O的直径，C是⊙O上一点，连接CB、CO．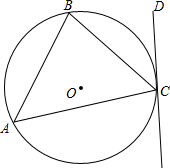
如图所示，A、B、C三点都在⊙O上，直线DE过点C，∠BCD=∠BAC，求证：DE与⊙O相切．
如图，∠CAB=∠CBD，AB=4，CB=5，AC=6，BD=7.5．求CD的长．