题目内容
在平面直角坐标系中，点P（2，5）与点Q关于x轴对称，则点Q的坐标是（ ）
| A、（-2，5） |
| B、（2，-5） |
| C、（-2，-5） |
| D、（5，2） |
考点：关于x轴、y轴对称的点的坐标
专题：
分析：根据平面直角坐标系中任意一点P（x，y），关于x轴的对称点的坐标是（x，-y），据此即可求得点P（2，5）关于x轴对称的点的坐标．
解答：解：∵点P（2，5）与点Q关于x轴对称，
∴点Q的坐标是（2，-5）．
故选：B．
∴点Q的坐标是（2，-5）．
故选：B．
点评：本题主要考查了直角坐标系点的对称性质，比较简单．
练习册系列答案
相关题目
如图，在梯形ABCD中，AB∥DC，DE∥CB，梯形的周长为28，△ADE周长为20，则DC=下列运算正确的是（ ）
A、-（-
| ||||
| B、-|-3|=3 | ||||
| C、（a2）3=a5 | ||||
| D、2a+3a=5a |
在平面直角坐标系中，点O是坐标原点，点A是x轴正半轴上的一个动点，过A点作y轴的平行线交反比例函数y=
（x＞0）的图象于B点，当点A的横坐标逐渐增大时，△OAB的面积将会（ ）
| 2 |
| x |
| A、逐渐增大 | B、逐渐减小 |
| C、不变 | D、先增大后减小 |
计算：
的结果是（ ）
| 22006 |
| 22005-22007 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
设m＞n＞0，m2+n2=3mn，则
的值等于（ ）
| m2-n2 |
| mn |
A、2
| ||
B、
| ||
C、2
| ||
D、
|
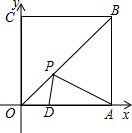如图所示，四边形OABC为正方形，边长为3，点A、C分别在x轴，y轴的正半轴上，点D在OA上，且D点的坐标为（1，0），P是OB上的一个动点，则PD+PA和的最小值是（ ）A、2
| ||
B、
| ||
| C、4 | ||
| D、9 |
已知正比例函数y=-4x与反比例函数y=
的图象交于A、B两点，若点A（m，4），则点B的坐标为（ ）
| k |
| x |
| A、（1，-4） |
| B、（-1，4） |
| C、（4，-1） |
| D、（-4，1） |
如图，正方形网格中，有格点三角形△ABC（顶点都是格点）和直线l．