题目内容
 如图,已知半径为1的圆的圆心为M(0,1),点B(0,2),A是x轴负半轴上的一点,D是OA的中点,AB交⊙M于点C,若四边形BCDM为平行四边形,则sin∠ABD=
如图,已知半径为1的圆的圆心为M(0,1),点B(0,2),A是x轴负半轴上的一点,D是OA的中点,AB交⊙M于点C,若四边形BCDM为平行四边形,则sin∠ABD=考点:圆的综合题
专题:
分析:连接BM,则平行四边形BCDM中证出DC∥OB,由BO⊥OA,DC⊥AO,结合D是AO的中点得到△ACO中AC=OC.由OB⊥x轴,因此得到△AOB是等腰直角三角形,故AO=OB=2.作DN⊥AB于N点,则△DNA是等腰直角三角形,且AD=1算出DN=
,在Rt△OBD中算出BD=
,从而可得Rt△BND中,sin∠ABD=
=
.
| ||
| 2 |
| 5 |
| DN |
| BD |
| ||
| 10 |
解答:解:连接OC,则
∵OB是⊙O的直径,∴∠OCB=90°,
∵四边形BCDM是平行四边形,
∴DC∥OB,
又∵BO⊥OA,
∴DC⊥AO,
∵D是AO的中点,
∴DC是△ACO的中线,
由此可得△ACO是等腰三角形,即AC=OC,
∵∠OCB=90°,
∴∠COA=∠A=45°,
因此得到Rt△AOB是等腰直角三角形,故AO=OB=2.
作DN⊥AB于N点,则△DNA是等腰直角三角形,且AD=1
∴DN=
∵Rt△OBD中,OB=2,OD=1,
∴BD=
=
=
,
故Rt△BND中,sin∠ABD=
=
.

∵OB是⊙O的直径,∴∠OCB=90°,
∵四边形BCDM是平行四边形,
∴DC∥OB,
又∵BO⊥OA,
∴DC⊥AO,
∵D是AO的中点,
∴DC是△ACO的中线,
由此可得△ACO是等腰三角形,即AC=OC,
∵∠OCB=90°,
∴∠COA=∠A=45°,
因此得到Rt△AOB是等腰直角三角形,故AO=OB=2.
作DN⊥AB于N点,则△DNA是等腰直角三角形,且AD=1
∴DN=
| ||
| 2 |
∵Rt△OBD中,OB=2,OD=1,
∴BD=
| OB2+OD2 |
| 22+12 |
| 5 |
故Rt△BND中,sin∠ABD=
| DN |
| BD |
| ||
| 10 |

点评:本题主要考查平行四边形的性质,圆的性质,等腰三角形的性质以及三角函数的判定.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,矩形ABCD为一本书,AB=12π,AD=2,当把书卷起时大致如图所示的半圆状(每张纸都是以O为圆心的同心圆的弧),如第一张纸AB对应为弧AB,最后一张纸CD对应为弧CD(CD为半圆),
如图,矩形ABCD为一本书,AB=12π,AD=2,当把书卷起时大致如图所示的半圆状(每张纸都是以O为圆心的同心圆的弧),如第一张纸AB对应为弧AB,最后一张纸CD对应为弧CD(CD为半圆), 如图,矩形ABCD的对角线AC和BD相交于点O,OA的垂直平分线BE恰好经过矩形的顶点B,求∠BAO的度数.
如图,矩形ABCD的对角线AC和BD相交于点O,OA的垂直平分线BE恰好经过矩形的顶点B,求∠BAO的度数.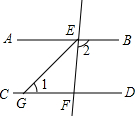 如图,已知AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠AEF,∠1=50°,求∠2的度数.
如图,已知AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠AEF,∠1=50°,求∠2的度数. 如图,正方形ABCD的面积为90.点P在AB上,PB=2PA;X,Y,Z三点在BD上,且BX=XY=YZ=ZD,则△PZX的面积为
如图,正方形ABCD的面积为90.点P在AB上,PB=2PA;X,Y,Z三点在BD上,且BX=XY=YZ=ZD,则△PZX的面积为 已知:如图,有一块边长为8m正方形的土地,上面修了横纵各两条路,宽度都是1m,空白部分种上各种花草,则种花草的面积
已知:如图,有一块边长为8m正方形的土地,上面修了横纵各两条路,宽度都是1m,空白部分种上各种花草,则种花草的面积