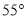��Ŀ����
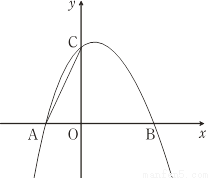
��ͼ�����κ���y=��x2+bx+c��ͼ����x�ύ�ڵ�A(��1��0)��B(2��0)����y���ཻ�ڵ�C��
��1������κ����Ľ���ʽ��
��2������E�ǵ�һ�����������ϵ�һ�����㣬���ı���ABEC��������ʱ�����E�����꣬������ı���ABEC����������
��3������M���������ϣ�����y����Ҳ࣮��M��y�����У��е�ΪD����C��D��MΪ��������������AOC���ƣ���ֱ��д����M�����꣮
��ϰ��ϵ�д�
�����Ŀ


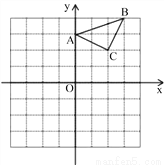
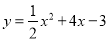 ��Ϊ
��Ϊ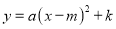 ����ʽ����__________������ͼ��������__________��
����ʽ����__________������ͼ��������__________��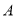 ��
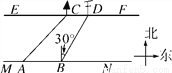
�� 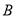 ��
�� 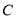 �ڡ�
�ڡ�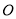 �ϣ�
�ϣ� 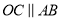 ��
�� 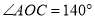 ����
����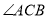 �Ķ���Ϊ��������
�Ķ���Ϊ��������
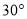 B.
B. 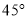 C.
C. 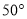 D.
D.