Question

18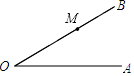．如图，∠AOB=30°，点M在OB上，且OM=5cm，以M为圆心，r为半径画圆，试讨论r的大小与所画⊙M和射线OA的公共点个数之间的对应关系．

Answer 1

分析 作MN⊥OA于N，如图，根据含30度的直角三角形三边的关系得到MN=$\frac{1}{2}$OM=$\frac{5}{2}$，然后根据直线与圆的关系得到当r=$\frac{5}{2}$时，⊙M与射线OA相切，只有一个公共点；当0＜r＜$\frac{5}{2}$时，⊙M与射线OA相离，没有公共点；当$\frac{5}{2}$＜r≤5时，⊙M与射线OA有两个公共点，而当r＞5时，⊙M与射线OA只有一个公共点．

解答 解：作MN⊥OA于N，如图，
∵∠AOB=30°，
∴MN=$\frac{1}{2}$OM=$\frac{1}{2}$×5=$\frac{5}{2}$，
∴当r=$\frac{5}{2}$时，⊙M与射线OA只有一个公共点；
当0＜r＜$\frac{5}{2}$时，⊙M与射线OA没有公共点；
当$\frac{5}{2}$＜r≤5时，⊙M与射线OA有两个公共点；
当r＞5时，⊙M与射线OA只有一个公共点．
所以当0＜r＜$\frac{5}{2}$时，⊙M与射线OA没有公共点；当r=$\frac{5}{2}$或r＞5时，⊙M与射线OA只有一个公共点；当$\frac{5}{2}$＜r≤5时，⊙M与射线OA有两个公共点．

点评 本题考查了直线和圆的位置关系：设⊙O的半径为r，圆心O到直线l的距离为d．若直线l和⊙O相交?d＜r；直线l和⊙O相切?d=r；直线l和⊙O相离?d＞r．