题目内容
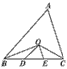
 如图,OD平分∠BOC,OE平分∠AOC,若∠BOC=70°,∠AOC=50°,请求出∠AOB与∠DOE的大小,并判断它们是否互补.
如图,OD平分∠BOC,OE平分∠AOC,若∠BOC=70°,∠AOC=50°,请求出∠AOB与∠DOE的大小,并判断它们是否互补.
解:∵OD平分∠BOC,∠BOC=70°,
∴∠BOD= ∠BOC=35°,
∠BOC=35°,
同理∠COE=25°,
∴∠DOE=∠COD+∠COE=60°,
∵∠BOC=70°,∠AOC=50°,
∴∠AOB=∠AOC+∠BOC=120°,
∴∠AOB+∠DOE=120°+60°=180°.
答:∠AOB与∠DOE互补.
分析:由于∠BOC=70°,∠AOC=50°,易求∠AOB,又OD平分∠BOC,∠BOC=70°,可求∠AOE,同理可求∠COE,进而可求∠DOE.
点评:本题考查了余角、补角,解题的关键是掌握角平分线的性质,并能理清角之间的和差关系.

∴∠BOD=
 ∠BOC=35°,
∠BOC=35°,同理∠COE=25°,
∴∠DOE=∠COD+∠COE=60°,
∵∠BOC=70°,∠AOC=50°,
∴∠AOB=∠AOC+∠BOC=120°,
∴∠AOB+∠DOE=120°+60°=180°.
答:∠AOB与∠DOE互补.
分析:由于∠BOC=70°,∠AOC=50°,易求∠AOB,又OD平分∠BOC,∠BOC=70°,可求∠AOE,同理可求∠COE,进而可求∠DOE.
点评:本题考查了余角、补角,解题的关键是掌握角平分线的性质,并能理清角之间的和差关系.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
 如图,在平面直角坐标系中,已知点B(-2
如图,在平面直角坐标系中,已知点B(-2 21、如图∠AOD=90°,OD为∠BOC的平分线,OE为BO的延长线,若∠AOB=40°,
21、如图∠AOD=90°,OD为∠BOC的平分线,OE为BO的延长线,若∠AOB=40°, 4、如图,AO⊥BO,射线OC平分∠AOB,射线OD平分∠BOC,射线OE平分∠AOD,则∠COE等于( )
4、如图,AO⊥BO,射线OC平分∠AOB,射线OD平分∠BOC,射线OE平分∠AOD,则∠COE等于( ) 12、如图,在△ABC中,BO、CO分别平分∠ABC和∠ACB,OD∥AB,OE∥AC,BC=14,则△ODE的周长=
12、如图,在△ABC中,BO、CO分别平分∠ABC和∠ACB,OD∥AB,OE∥AC,BC=14,则△ODE的周长=