题目内容
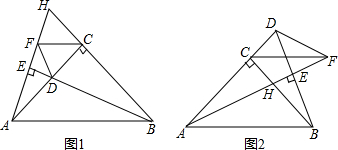
在Rt△ABC中,∠ACB=90°,AC=BC,D为直线AC上一点,直线AE⊥直线BD,垂足为E,直线AE和直线BC交于点H,过点C作AB的平行线,交直线AE于F,连DF.
(1)若D在线段AC上(如图1),求证:∠CDB=∠CDF;
(2)若D在AC延长线上(如图2),求证:∠CDB+∠CDF=180°.
(1)若D在线段AC上(如图1),求证:∠CDB=∠CDF;
(2)若D在AC延长线上(如图2),求证:∠CDB+∠CDF=180°.

考点:全等三角形的判定与性质
专题:证明题
分析:(1)求出∠3=∠4,∠1=∠2,根据ASA推出△ACH≌△BCD,推出CH=CD,∠H=∠CDB,根据SAS推出△CHF≌△CDF,推出∠H=∠CDF即可;
(2)求出∠3=∠4,∠1=∠2,根据ASA推出△ACH≌△BCD,推出CH=CD,∠H=∠CDB,根据SAS推出△CHF≌△CDF,推出∠CHF=∠CDF即可.
(2)求出∠3=∠4,∠1=∠2,根据ASA推出△ACH≌△BCD,推出CH=CD,∠H=∠CDB,根据SAS推出△CHF≌△CDF,推出∠CHF=∠CDF即可.
解答:
证明:(1)∵在Rt△ABC中,∠ACB=90°,AB=AC,
∴∠BAC=∠ABC=45°,∠ACH=90°,
∵CF∥AB,
∴∠4=∠BAC=45°,∠3=∠ABC=45°,
∴∠3=∠4,
∴在Rt△ACH中,∠1+∠H=90°,
∵AE⊥BD,
∴在Rt△BEH中,∠2+∠H=90°,
∴∠1=∠2,
在△ACH和△BCD中,
,
∴△ACH≌△BCD(ASA),
∴CH=CD,∠H=∠CDB,
在△CHF和△CDF中
∴△CHF≌△CDF(SAS),
∴∠H=∠CDF,
∴∠CDB=∠CDF;
(2)∵在Rt△ABC中,∠ACB=90°,AB=AC,
∴∠BAC=∠ABC=45°,∠ACH=90°,
∵CF∥AB,
∴∠4=∠BAC=45°,∠3=∠ABC=45°,
∴∠3=∠4,
∴在Rt△ADE中,∠1+∠ADE=90°,
∵AE⊥BD,
∴在Rt△BEH中,∠2+∠ADE=90°,
∴∠1=∠2,
在△ACH和△BCD中
,
∴△ACH≌△BCD(ASA),
∴CH=CD,∠ACH=∠CDB,
在△CHF和△CDF中
∴△CHF≌△CDF(SAS),
∴∠CHF=∠CDF,
∵∠DCH+∠CHE+∠DEH+∠CDE=360°,
∴∠ACH+∠CHF=180°,
∴∠CDB+∠CDF=180°.

证明:(1)∵在Rt△ABC中,∠ACB=90°,AB=AC,
∴∠BAC=∠ABC=45°,∠ACH=90°,
∵CF∥AB,
∴∠4=∠BAC=45°,∠3=∠ABC=45°,
∴∠3=∠4,
∴在Rt△ACH中,∠1+∠H=90°,
∵AE⊥BD,
∴在Rt△BEH中,∠2+∠H=90°,
∴∠1=∠2,
在△ACH和△BCD中,
|
∴△ACH≌△BCD(ASA),
∴CH=CD,∠H=∠CDB,
在△CHF和△CDF中
|
∴△CHF≌△CDF(SAS),
∴∠H=∠CDF,
∴∠CDB=∠CDF;
(2)∵在Rt△ABC中,∠ACB=90°,AB=AC,
∴∠BAC=∠ABC=45°,∠ACH=90°,
∵CF∥AB,
∴∠4=∠BAC=45°,∠3=∠ABC=45°,
∴∠3=∠4,
∴在Rt△ADE中,∠1+∠ADE=90°,
∵AE⊥BD,
∴在Rt△BEH中,∠2+∠ADE=90°,
∴∠1=∠2,
在△ACH和△BCD中
|
∴△ACH≌△BCD(ASA),
∴CH=CD,∠ACH=∠CDB,
在△CHF和△CDF中
|
∴△CHF≌△CDF(SAS),
∴∠CHF=∠CDF,
∵∠DCH+∠CHE+∠DEH+∠CDE=360°,
∴∠ACH+∠CHF=180°,
∴∠CDB+∠CDF=180°.
点评:本题考查了三角形内角和定理和全等三角形的性质和判定的应用,题目比较好,证明过程类似.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
 如图,将一副三角尺如图所示叠放在一起,若AB=12cm,则阴影部分的面积是( )
如图,将一副三角尺如图所示叠放在一起,若AB=12cm,则阴影部分的面积是( )| A、12 | B、18 | C、24 | D、36 |
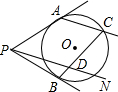 如图,PA与PB切⊙O于A、B,C为优弧
如图,PA与PB切⊙O于A、B,C为优弧
 在△ABC中,∠C=90°,AC=6,BC=8,DE垂直平分AB,求BE的长.
在△ABC中,∠C=90°,AC=6,BC=8,DE垂直平分AB,求BE的长. 如图,四边形ABCD中,∠A=60°,则∠1+∠2=
如图,四边形ABCD中,∠A=60°,则∠1+∠2=