题目内容
11.已知$\frac{x}{y}$=$\frac{4}{5}$,则$\frac{3x}{x+y}$的值为$\frac{4}{3}$.分析 根据等式的性质,可用y表示x,根据分式的性质,可得答案.
解答 解:由题意,得
x=$\frac{4}{5}$y.
$\frac{3x}{x+y}$=$\frac{3×\frac{4}{5}y}{\frac{4}{5}y+y}$=$\frac{4}{3}$,
故答案为:$\frac{4}{3}$.
点评 本题考查了比例的性质,利用等式的性质得出x=$\frac{4}{5}$y是解题关键.

练习册系列答案
相关题目
6. 两个反比例函数y=$\frac{k}{x}$和y=$\frac{1}{x}$在第一象限内,点P在y=$\frac{k}{x}$的图象上,PC垂直于X轴于点C,交y=$\frac{1}{x}$的图象于点A,PD垂直于Y轴于D,交y=$\frac{1}{x}$的图象于点B,当点P在y=$\frac{k}{x}$的图象上运动时,下列结论错误的是( )
两个反比例函数y=$\frac{k}{x}$和y=$\frac{1}{x}$在第一象限内,点P在y=$\frac{k}{x}$的图象上,PC垂直于X轴于点C,交y=$\frac{1}{x}$的图象于点A,PD垂直于Y轴于D,交y=$\frac{1}{x}$的图象于点B,当点P在y=$\frac{k}{x}$的图象上运动时,下列结论错误的是( )
 两个反比例函数y=$\frac{k}{x}$和y=$\frac{1}{x}$在第一象限内,点P在y=$\frac{k}{x}$的图象上,PC垂直于X轴于点C,交y=$\frac{1}{x}$的图象于点A,PD垂直于Y轴于D,交y=$\frac{1}{x}$的图象于点B,当点P在y=$\frac{k}{x}$的图象上运动时,下列结论错误的是( )
两个反比例函数y=$\frac{k}{x}$和y=$\frac{1}{x}$在第一象限内,点P在y=$\frac{k}{x}$的图象上,PC垂直于X轴于点C,交y=$\frac{1}{x}$的图象于点A,PD垂直于Y轴于D,交y=$\frac{1}{x}$的图象于点B,当点P在y=$\frac{k}{x}$的图象上运动时,下列结论错误的是( )| A. | △ODB与△OCA的面积相等 | |
| B. | 当点A是PC的中点时,点B一定是PD的中点 | |
| C. | 只有当四边形OCPB为正方形时,四边形PAOB的面积最大 | |
| D. | $\frac{CA}{PA}$=$\frac{DB}{PB}$ |
20.下列各组数,能构成直角三角形边的是( )
| A. | 4,5,6 | B. | 8,15,17 | C. | 5,8,10 | D. | 8,39,40 |
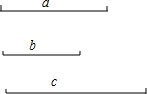 已知线段a,b,c.如图,求作线段x,使x=$\frac{3bc}{2a}$.
已知线段a,b,c.如图,求作线段x,使x=$\frac{3bc}{2a}$.