题目内容
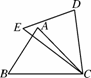
如图4222,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连接AE,DE,DC.
(1)求证:△ABE≌△CBD;
(2)若∠CAE=30°,求∠BDC的度数.

(1)证明:∵∠ABC=90°,∴∠DBE=180°-∠ABC=90°.
∴∠ABE=∠CBD.
在△ABE和△CBD中,
 ∴△ABE≌△CBD(SAS).
∴△ABE≌△CBD(SAS).
(2)解:∵AB=CB,∠ABC=90°,
∴△ABC是等腰直角三角形.∴∠ECA=45°.
∵∠CAE=30°,∠BEA=∠ECA+∠EAC,
∴∠BEA=45°+30°=75°.
由①知∠BDC=∠BEA,∴∠BDC=75°.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
 与直线
与直线 在第二象限的交点,AB垂直
在第二象限的交点,AB垂直 轴于点B,且S△ABO=
轴于点B,且S△ABO= ;(1)求两个函数的表达式
;(1)求两个函数的表达式
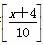 =5,则x的取值可以是( )
=5,则x的取值可以是( )