题目内容
14.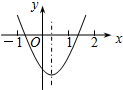 如图,抛物线y=ax2+bx+c的对称轴是x=$\frac{1}{3}$,小亮通过观察得出了下面四条信息:
如图,抛物线y=ax2+bx+c的对称轴是x=$\frac{1}{3}$,小亮通过观察得出了下面四条信息:①4ac-b2>0,②abc<0,③4a+2b+c>0,④2a+3b=0.你认为其中正确的有( )
| A. | ①② | B. | ②④ | C. | ①③ | D. | ③④ |
分析 根据抛物线的开口方向,对称轴,与y轴的交点位置,x=-1时的函数值的情况,逐一判断.
解答 解:A、由抛物线开口向上,与x轴有两个交点,可知b2-4ac>0,故本选项错误;
B、由抛物线的开口向上知,a>0,对称轴为x=-$\frac{b}{2a}$>0,a、b异号,即b<0,∴abc>0,故本选项错误;
C、当x=2时,4a+2b+c>0,故本选项正确;
D、由对称轴为x=-$\frac{b}{2a}$=$\frac{1}{3}$,得2a+3b=0,故本选项正确.
故选:D.
点评 本题主要考查了二次函数图象与系数的关系,二次函数y=ax2+bx+c系数符号由抛物线开口方向、对称轴及抛物线与y轴的交点确定.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
4.-|-2|的相反数的倒数是( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | -2 |
9.下列图形中,既不是轴对称图形,又不是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
3.已知点A(-2,1),B(1,4),若反比例函数y=$\frac{k}{x}$与线段AB有公共点时,k的取值范围是( )
| A. | -$\frac{9}{4}$≤k<0或0<k≤4 | B. | k≤-2或k≥4 | C. | -2≤k<0或k≥4 | D. | -2≤k<0或0<k≤4 |
4.下列说法正确的是( )
| A. | “打开电视机,它正在播《奔跑吧,兄弟》”是必然事件 | |
| B. | “一个不透明的袋中装有8个红球,从中摸出一个球是红球”是随机事件 | |
| C. | 为了了解我市今年夏季家电市场中空调的质量,不宜采用普查的调查方式进行 | |
| D. | 销售某种品牌的凉鞋,销售商最感兴趣的是该品牌凉鞋的尺码的平均数 |
 (1)如图,EF∥AD,∠1=∠2,∠BAC=80°.将求∠AGD的过程填写完整.
(1)如图,EF∥AD,∠1=∠2,∠BAC=80°.将求∠AGD的过程填写完整.
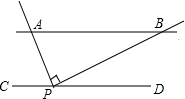 如图,AB∥CD,点P在CD上,且AP⊥BP,∠ABP=25°,则∠APC=65度.
如图,AB∥CD,点P在CD上,且AP⊥BP,∠ABP=25°,则∠APC=65度.