Question

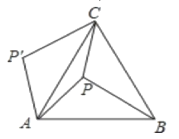
【题目】如图,P是等边△ABC内一点,且PA=6,PC=8,PB=10,若△APB绕点A逆时针旋转60后,得到△AP′C,则∠APC=（ ）.

A.150°B.120°C.100°D.110°

Answer 1

【答案】A

【解析】

连接PP′，根据旋转变换的性质可得△AP′C和△APB全等，根据全等三角形对应边相等可得P′A=PA，P′C=PB，然后证明△APP′是等边三角形，根据等边三角形的每一个角都是60°可得∠APP′=60°，每一条边都相等可得PP′=PA，再根据勾股定理逆定理证明△P′PC是直角三角形，然后根据∠APC=∠APP′+∠P′PC代入数据进行计算即可得解．

如图,连接PP′，

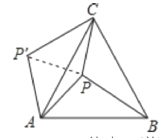
∵△APB绕点A逆时针旋转60°得到△AP′C，

∴△AP′C≌△APB，

∴P′A=PA=6,P′C=PB=10，

∵旋转角是60，

∴△APP′是等边三角形，

∴∠APP′=60,PP′=PA=6，

∵PP′+PC=6+8=100,P′C=PB=10=100，

∴PP′+PC=P′C，

∴△P′PC是以∠P′PC为直角的直角三角形，

∴∠APC=∠APP′+∠P′PC=60+90=150°.

故答案为：A