题目内容
1.已知二次函数y=-x2-2bx+c,当x<2时,y的值随x的增大而增大,则实数b的取值范围是( )| A. | b≥-1 | B. | b≤-1 | C. | b≥-2 | D. | b≤-2 |
分析 先利用二次函数的性质求出抛物线的对称轴为直线x=-b,则当x<-b时,y的值随x值的增大而增大,由于x<2时,y的值随x值的增大而增大,于是得到-b≥2.
解答 解:解:抛物线的对称轴为直线x=-$\frac{-2b}{-2}$=-b,
因为a=-1<0,
所以抛物线开口向下,
所以当x<-b时,y的值随x值的增大而增大,
而x<2时,y的值随x值的增大而增大,
所以-b≥2.
b≤-2
故选D.
点评 本题考查了二次函数的性质,主要利用了二次函数的增减性,熟记性质并列出不等式是解题的关键.

练习册系列答案
相关题目
11.解分式方程$\frac{1}{x-1}$-2=$\frac{3}{1-x}$,去分母得( )
| A. | 1-2(x-1)=-3 | B. | 1-2(x-1)=3 | C. | 1-2x-2=-3 | D. | 1-2x+2=3 |
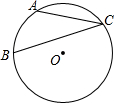 如图,点A、B、C在半径为1的⊙O上,$\widehat{AB}$的长为$\frac{2}{5}$π,则∠ACB的大小是36°.
如图,点A、B、C在半径为1的⊙O上,$\widehat{AB}$的长为$\frac{2}{5}$π,则∠ACB的大小是36°.
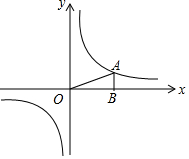 如图,已知反比例函数y=$\frac{k}{x}$的图象经过点A(4,m),AB⊥x轴,且△AOB的面积为2.
如图,已知反比例函数y=$\frac{k}{x}$的图象经过点A(4,m),AB⊥x轴,且△AOB的面积为2. 如图,△ABC内接于⊙O,若∠OAB=26°,则∠C的大小为64°.
如图,△ABC内接于⊙O,若∠OAB=26°,则∠C的大小为64°.