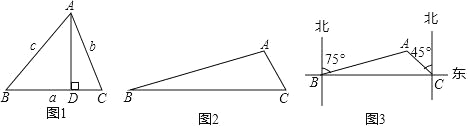
ЬтФПФкШн
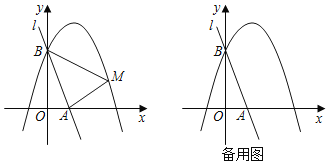
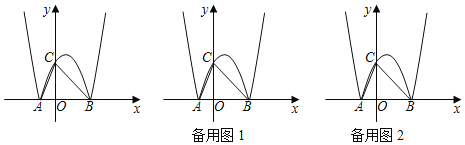
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯпyЃНx2Љ2xЉ3НЛxжсгкAЃЌBСНЕуЃЈЕуAдкЕуBЕФзѓВрЃЉЃЌНЋИУХзЮяЯпЮЛгкxжсЩЯЗНЕФЧњЯпМЧзїMЃЌНЋИУХзЮяЯпЮЛгкxжсЯТЗНЕФВПЗжбиxжсЗелЃЌЗелКѓЫљЕУЧњЯпМЧзїNЃЌЧњЯпNНЛyжсгкЕуCЃЌСЌНгACЃЌBCЃЎ
ЃЈ1ЃЉЧѓЧњЯпNЫљдкХзЮяЯпЕФКЏЪ§БэДяЪНЃЛ
ЃЈ2ЃЉЧѓЁїABCЭтНгдВЕФУцЛ§ЃЛ
ЃЈ3ЃЉЕуPЮЊЧњЯпMЛђЧњЯпNЩЯЕФЖЏЕуЃЌЕуQЮЊxжсЩЯЕФвЛИіЖЏЕуЃЌШєвдЕуBЃЌCЃЌPЃЌQЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЌЧыжБНгаДГіЕуQЕФзјБъЃЛ
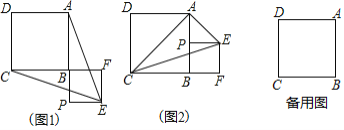
ЃЈ4ЃЉдкжБЯпBCЩЯЗНЕФЧњЯпMЩЯШЗЖЈСНИіЕуD1ЃЌD2ЃЌЪЙЕУ![]() ЃН
ЃН![]() ЃНSЁїABCЃЎВЂЧѓГіЕуD1ЃЌD2ЕФзјБъЃЛдкЧњЯпMЛђNЩЯЪЧЗёДцдкЮхИіЕуT1ЃЌT2ЃЌT3ЃЌT4ЃЌT5ЃЌЪЙЕУетЮхИіЕуЗжБ№гыЕуBЃЌCЮЇГЩЕФШ§НЧаЮЕФУцЛ§ЮЊ
ЃНSЁїABCЃЎВЂЧѓГіЕуD1ЃЌD2ЕФзјБъЃЛдкЧњЯпMЛђNЩЯЪЧЗёДцдкЮхИіЕуT1ЃЌT2ЃЌT3ЃЌT4ЃЌT5ЃЌЪЙЕУетЮхИіЕуЗжБ№гыЕуBЃЌCЮЇГЩЕФШ§НЧаЮЕФУцЛ§ЮЊ![]() ЃПШєДцдкЃЌжБНгаДГіетЮхИіЕуT1ЃЌT2ЃЌT3ЃЌT4ЃЌT5ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЃПШєДцдкЃЌжБНгаДГіетЮхИіЕуT1ЃЌT2ЃЌT3ЃЌT4ЃЌT5ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉyЃНЉx2+2x+3ЃЛЃЈ2ЃЉ5ІаЃЛЃЈ3ЃЉQЃЈ1ЃЌ0ЃЉЛђQЃЈ2Љ![]() ЃЌ0ЃЉЛђQЃЈ2+
ЃЌ0ЃЉЛђQЃЈ2+![]() ЃЌ0ЃЉЪБвдЕуBЃЌCЃЌPЃЌQЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЛЃЈ4ЃЉДцдкЃЌT1ЃЈЉ
ЃЌ0ЃЉЪБвдЕуBЃЌCЃЌPЃЌQЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЛЃЈ4ЃЉДцдкЃЌT1ЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉЛђT2ЃЈ
ЃЉЛђT2ЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЛђT3ЃЈ
ЃЉЛђT3ЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЛђT4ЃЈ
ЃЉЛђT4ЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЛђT5ЃЈ
ЃЉЛђT5ЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉгЩNгыMЭМЯѓЯТЗНЕФВПЗжЙигкxжсЖдГЦЃЌдђПЩЧѓNЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЧѓГіAЁЂBЁЂCЕузјБъЃЌЗжБ№зїBCгыABЕФДЙжБЦНЗжЯпНЛгкЕуO'ЃЌдђO'ЮЊЁїABCЕФЭтНгдВЃЌгЩЕШбќШ§НЧаЮЕФаджЪКЭЙДЙЩЖЈРэПЩЧѓЭтНгдВАыОЖЃЛ
ЃЈ3ЃЉЗжСНжжЧщПіЃКЕБPЕудкMЩЯЪБЃЌЩшPЃЈmЃЌm2Љ2mЉ3ЃЉЃЌQЃЈnЃЌ0ЃЉЃЌЕБPЕудкNЩЯЪБЃЌЩшPЃЈmЃЌЉm2+2m+3ЃЉЃЌQЃЈnЃЌ0ЃЉЃЌдйдкУПжжЧщПіжаЗжСНжжЧщПіЂйЕБBQЁЮPCЃЌBQЃНPCЪБЃЌЂкЕБBPЁЮCQЃЌBPЃНCQЪБЃЌРћгУЦНааЫФБпаЮЖдНЧЯпЛЅЯрЦНЗжЕФаджЪЃЌжаЕужиКЯСЊСЂЗНГЬзщЧѓНтЃЛ
ЃЈ4ЃЉгЩвбжЊПЩЕУD1D2ЫљдкжБЯпгыжБЯпBCЦНааЃЌD1D2ЫљдкжБЯпгыжБЯпBCМфЕФОрРыЮЊ2![]() ЃЌЩшD1D2ЕФжБЯпНтЮіЪНЮЊyЃНЉx+bЃЌгЩbЉ3ЃН4ЃЌПЩЧѓyЃНЉx+7ЃЌдйгыХзЮяЯпСЊСЂЗНГЬзщМДПЩЧѓD1ЁЂD2ЕузјБъЃЛT1ЃЌT2ЃЌT3ЃЌT4ЃЌT5ЕНжБЯпBCЕФОрРыЮЊ
ЃЌЩшD1D2ЕФжБЯпНтЮіЪНЮЊyЃНЉx+bЃЌгЩbЉ3ЃН4ЃЌПЩЧѓyЃНЉx+7ЃЌдйгыХзЮяЯпСЊСЂЗНГЬзщМДПЩЧѓD1ЁЂD2ЕузјБъЃЛT1ЃЌT2ЃЌT3ЃЌT4ЃЌT5ЕНжБЯпBCЕФОрРыЮЊ![]() ЃЌЩшгыBCЦНааЕФжБЯпЮЊyЃНЉx+tЃЌдђ|tЉ3|ЃН
ЃЌЩшгыBCЦНааЕФжБЯпЮЊyЃНЉx+tЃЌдђ|tЉ3|ЃН![]() ЃЌдђЮхИіЕуЗжБ№дкжБЯпyЃНЉx+
ЃЌдђЮхИіЕуЗжБ№дкжБЯпyЃНЉx+![]() ЛђyЃНЉx+
ЛђyЃНЉx+![]() ЩЯЃЌдйНЋжБЯпгыMЁЂNЕФНтЮіЪНСЊСЂМДПЩЧѓзјБъЃЎ
ЩЯЃЌдйНЋжБЯпгыMЁЂNЕФНтЮіЪНСЊСЂМДПЩЧѓзјБъЃЎ
НтЃКЃЈ1ЃЉЁпNгыMЭМЯѓЯТЗНЕФВПЗжЙигкxжсЖдГЦЃЌ
ЁрNЫљдкКЏЪ§НтЮіЪНЮЊyЃНЉx2+2x+3ЃЛ
ЃЈ2ЃЉСюx2Љ2xЉ3ЃН0ЃЌНтЕУxЃНЉ1ЛђxЃН3ЃЌ
ЁрAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉЃЌ
ЁпЧњЯпNНЛyжсгкЕуCЃЌ
ЁрCЃЈ0ЃЌ3ЃЉЃЌ
ЗжБ№зїBCгыABЕФДЙжБЦНЗжЯпНЛгкЕуO'ЃЌдђO'ЮЊЁїABCЕФЭтНгдВЃЌ
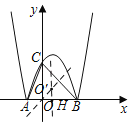
ЁпRtЁїBOCЮЊЕШбќжБНЧШ§НЧаЮЃЌ
ЁрOO'ЃНOHЃНO'HЃН1ЃЌ
ЁпHBЃН2ЃЌ
ЁрO'BЃН![]() ЃЌ
ЃЌ
ЁпO'BЪЧЁїABCЭтНгдВЕФАыОЖЃЌ
ЁрЁїABCЭтНгдВЕФУцЛ§ЃН5ІаЃЛ
ЃЈ3ЃЉЕБPЕудкMЩЯЪБЃЌЩшPЃЈmЃЌm2Љ2mЉ3ЃЉЃЌQЃЈnЃЌ0ЃЉЃЌ
ЁрmЁн3ЛђmЁмЉ1ЃЛ
ЂйЕБBQЁЮPCЃЌBQЃНPCЪБЃЌBЁЂCЕФжаЕуЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌPЁЂQЕФжаЕуЮЊЃЈ
ЃЉЃЌPЁЂQЕФжаЕуЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
Ёр![]() ЃН
ЃН![]() ЃЌНтЕУmЃН1+
ЃЌНтЕУmЃН1+![]() ЛђmЃН1Љ
ЛђmЃН1Љ![]() ЃЌ
ЃЌ
![]() ЃН
ЃН![]() ЃЌНтЕУnЃН2Љ
ЃЌНтЕУnЃН2Љ![]() ЛђnЃН2+
ЛђnЃН2+![]() ЃЌ
ЃЌ
ЁрQЃЈ2Љ![]() ЃЌ0ЃЉЛђQЃЈ2+
ЃЌ0ЃЉЛђQЃЈ2+![]() ЃЌ0ЃЉЃЛ
ЃЌ0ЃЉЃЛ
ЂкЕБBPЁЮCQЃЌBPЃНCQЪБЃЌBЁЂQЕФжаЕуЮЊЃЈ![]() ЃЌ0ЃЉЃЌPЁЂCЕФжаЕуЮЊЃЈ
ЃЌ0ЃЉЃЌPЁЂCЕФжаЕуЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
Ёр![]() ЃН0ЃЌНтЕУmЃН0ЛђmЃН2ЃЈЖМВЛЗћКЯЃЉЃЛ
ЃН0ЃЌНтЕУmЃН0ЛђmЃН2ЃЈЖМВЛЗћКЯЃЉЃЛ
ЕБPЕудкNЩЯЪБЃЌЩшPЃЈmЃЌЉm2+2m+3ЃЉЃЌQЃЈnЃЌ0ЃЉЃЌ
ЁрЉ1ЁмmЁм3ЃЌ
ЂлЕБBQЁЮPCЃЌBQЃНPCЪБЃЌBЁЂCЕФжаЕуЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌPЁЂQЕФжаЕуЮЊЃЈ
ЃЉЃЌPЁЂQЕФжаЕуЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
Ёр![]() ЃН
ЃН![]() ЃЌНтЕУmЃН0ЛђmЃН2ЃЌ
ЃЌНтЕУmЃН0ЛђmЃН2ЃЌ
![]() ЃН
ЃН![]() ЃЌНтЕУnЃН3ЛђnЃН1ЃЌ
ЃЌНтЕУnЃН3ЛђnЃН1ЃЌ
ЁрQЃЈ1ЃЌ0ЃЉЛђQЃЈ3ЃЌ0ЃЉЃЌ
ЁпQЃЈ3ЃЌ0ЃЉгыBЃЈ3ЃЌ0ЃЉжиКЯЃЌ
ЁрQЃЈ1ЃЌ0ЃЉЃЛ
ЂмЕБBPЁЮCQЃЌBPЃНCQЪБЃЌBЁЂQЕФжаЕуЮЊЃЈ![]() ЃЌ0ЃЉЃЌPЁЂCЕФжаЕуЮЊЃЈ
ЃЌ0ЃЉЃЌPЁЂCЕФжаЕуЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
Ёр![]() ЃН0ЃЌНтЕУmЃН1+
ЃН0ЃЌНтЕУmЃН1+![]() ЛђmЃН1Љ
ЛђmЃН1Љ![]() ЃЈЖМВЛЗћКЯЃЉЃЛ
ЃЈЖМВЛЗћКЯЃЉЃЛ
злЩЯЫљЪіЃКQЃЈ1ЃЌ0ЃЉЛђQЃЈ2Љ![]() ЃЌ0ЃЉЛђQЃЈ2+
ЃЌ0ЃЉЛђQЃЈ2+![]() ЃЌ0ЃЉЪБвдЕуBЃЌCЃЌPЃЌQЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЛ
ЃЌ0ЃЉЪБвдЕуBЃЌCЃЌPЃЌQЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЛ
ЃЈ4ЃЉЁп![]() ЃН
ЃН![]() ЃНSЁїABCЃЌ
ЃНSЁїABCЃЌ
ЁрD1D2ЫљдкжБЯпгыжБЯпBCЦНааЃЌ
ЁпBCЃН3![]() ЃЌ
ЃЌ
ЩшAЕуЕНBCЕФОрРыЮЊhЃЌ
ЁпЁїABCЕФУцЛ§ЃН![]() ЁС3
ЁС3![]() hЃН
hЃН![]() ЁС4ЁС3ЃЌ
ЁС4ЁС3ЃЌ
ЁрhЃН2![]() ЃЌ
ЃЌ
ЁрD1D2ЫљдкжБЯпгыжБЯпBCМфЕФОрРыЮЊ2![]() ЃЌ
ЃЌ
ЩшD1D2ЕФжБЯпНтЮіЪНЮЊyЃНЉx+bЃЌ
ЁрbЉ3ЃН4ЃЌ
ЁрbЃН7ЃЌ
ЁрyЃНЉx+7ЃЌ
СЊСЂ![]() ЃЌНтЕУxЃН
ЃЌНтЕУxЃН![]() ЛђxЃН
ЛђxЃН![]() ЃЌ
ЃЌ
ЁрD1ЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌD2ЃЈ
ЃЉЃЌD2ЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЛ
ЃЉЃЛ
СЊСЂ![]() ЃЌНтЕУxЮоНтЃЛ
ЃЌНтЕУxЮоНтЃЛ
злЩЯЫљЪіЃКD1ЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌD2ЃЈ
ЃЉЃЌD2ЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЛ
ЃЉЃЛ
ЁпT1ЃЌT2ЃЌT3ЃЌT4ЃЌT5гыЕуBЃЌCЮЇГЩЕФШ§НЧаЮЕФУцЛ§ЮЊ![]() ЃЌ
ЃЌ
ЁрT1ЃЌT2ЃЌT3ЃЌT4ЃЌT5ЕНжБЯпBCЕФОрРыЮЊ![]() ЃЌ
ЃЌ
ЩшгыBCЦНааЕФжБЯпЮЊyЃНЉx+tЃЌ
Ёр|tЉ3|ЃН![]() ЃЌ
ЃЌ
ЁрtЃН![]() ЛђtЃН
ЛђtЃН![]() ЃЌ
ЃЌ
ЁрyЃНЉx+![]() ЛђyЃНЉx+
ЛђyЃНЉx+![]() ЃЌ
ЃЌ
ЕБЕудкMЩЯЪБЃЌxЁн3ЛђxЁмЉ1ЃЌ
СЊСЂ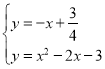 ЃЌНтЕУxЃН
ЃЌНтЕУxЃН![]() ЛђxЃНЉ
ЛђxЃНЉ![]() ЃЌ
ЃЌ
ЁрxЃНЉ![]() ЃЌ
ЃЌ
ЁрT1ЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉЃЛ
ЃЉЃЛ
СЊСЂ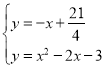 ЃЌНтЕУxЃН
ЃЌНтЕУxЃН![]() ЛђxЃН
ЛђxЃН![]() ЃЌ
ЃЌ
ЁрT2ЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЛђT3ЃЈ
ЃЉЛђT3ЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЛ
ЃЉЃЛ
ЕБЕудкNЩЯЪБЃЌЉ1ЁмxЁм3ЃЌ
СЊСЂ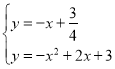 ЃЌНтЕУxЃН
ЃЌНтЕУxЃН![]() ЃЈЩсЃЉЛђxЃН
ЃЈЩсЃЉЛђxЃН![]() ЃЌ
ЃЌ
ЁрT4ЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЛ
ЃЉЃЛ
СЊСЂ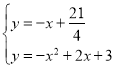 ЃЌНтЕУxЃН
ЃЌНтЕУxЃН![]() ЃЌ
ЃЌ
ЁрT5ЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЛ
ЃЉЃЛ
злЩЯЫљЪіЃКДцдкЮхИіЕуЗћКЯЬѕМўЃЌЗжБ№ЪЧT1ЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉЛђT2ЃЈ
ЃЉЛђT2ЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЛђT3ЃЈ
ЃЉЛђT3ЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЛђT4ЃЈ
ЃЉЛђT4ЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЛђT5ЃЈ
ЃЉЛђT5ЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ

 Н№зДдЊМЈгХКУОэЯЕСаД№АИ
Н№зДдЊМЈгХКУОэЯЕСаД№АИ