题目内容
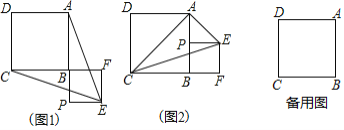
【题目】已知正方形ABCD，P为射线AB上的一点，以BP为边作正方形BPEF，使点F在线段CB的延长线上，连接EA、EC．
（1）如图1，若点P在线段AB的延长线上，求证：EA=EC；
（2）若点P在线段AB上，如图2，当点P为AB的中点时，判断△ACE的形状，并说明理由；
（3）在（1）的条件下，将正方形ABCD固定，正方形BPEF绕点B旋转一周，设AB=4，BP=a，若在旋转过程中△ACE面积的最小值为4，请直接写出a的值．
【答案】（1）见解析；（2）△ACE是直角三角形，理由见解析；（3）a=1．
【解析】
（1）根据正方形的性质和全等三角形的判定定理证明△APE≌△CFE，根据全等三角形的性质证明结论；
（2）根据正方形的性质、等腰直角三角形的性质解答；
（3）连接BD、AC交于点O．点E的运动轨迹是以B为圆心，
a为半径的圆，则当点E在对角线BD上时，△ACE的面积最小， 根据
×AC×OE=4，得到OE=，即可求出BE=2–=，进而求出 a=1．
（1）如图1中，
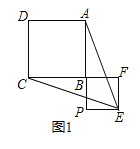
∵四边形ABCD和四边形BPEF是正方形，
∴AB=BC，BP=BF，∴AP=CF，
在△APE和△CFE中，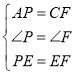
，
∴△APE≌△CFE，
∴EA=EC；
（2）△ACE是直角三角形，
理由如下：如图2中，
∵P为AB的中点，∴PA=PB，
∵PB=PE，∴PA=PE，∴∠PAE=45°，
又∵∠BAC=45°，
∴∠CAE=90°，即△ACE是直角三角形；
（3）如图3，连接BD、AC交于点O．
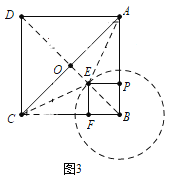
∵点E的运动轨迹是以B为圆心，a为半径的圆，
∴当点E在对角线BD上时，△ACE的面积最小，
∵×AC×OE=4，∴OE=，
∵BE=2–=，∴a=1．
练习册系列答案
相关题目
