题目内容
2.某房地产开发公司计划建A、B两种户型的经济适用住房共80套,该公司所筹资金不少于2090万元,但不超过2096万元,且所筹资金全部用于建房,两种户型的建房成本和售价如表:| A | B | |
| 成本(万元/套) | 25 | 28 |
| 售价(万元/套) | 30 | 34 |
(2)若该公司所建的两种户型住房可全部售出,则采取哪一种建房方案获得利润最大?
分析 (1)首先设A种户型的住房建x套,则B种户型的住房建(80-x)套,然后根据题意列不等式组,解不等式组可求得x的取值范围,又由x取非负整数,即可求得x的可能取值,则可得到三种建房方案;
(2)设该公司建房获得利润W万元,根据题意可得W与x的一次函数关系式,则可求得何时获得利润最大.
解答 解:(1)设A种户型的住房建x套,则B种户型的住房建(80-x)套.
根据题意,得
$\left\{\begin{array}{l}{25x+28(80-x)≥2090}\\{25x+28(80-x)≤2096}\end{array}\right.$,
解得48≤x≤50.
∵x取非负整数,
∴x为48,49,50.
∴有三种建房方案:
| 方案① | 方案② | 方案③ | |
| A型 | 48套 | 49套 | 50套 |
| B型 | 32套 | 31套 | 30套 |
由题意知:W=5x+6(80-x)=480-x,
∵k=-1,W随x的增大而减小,
∴当x=48时,即A型住房建48套,B型住房建32套获得利润最大.
点评 此题考查了一元一次不等式组与一次函数的实际应用.解题的关键是理解题意,注意利用一次函数求最值时,关键是应用一次函数的性质;即由函数y随x的变化,结合自变量的取值范围确定最值.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
9.若a>b,则下列各式中一定成立的是( )
| A. | ma>mb | B. | a2>b2 | C. | 1-a>1-b | D. | b-a<0 |
10.下列图形中,不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
10.中国现行的个人所得税法自 2011年9月1日起施行,其中规定个人所得税纳税办法如下:
一、以个人每月工资收入额减去 3500元后的余额作为其每月应纳税所得额;
二、个人所得税纳税税率如下表所示:
(1)若甲、乙两人的每月工资收入额分别为4500元和6000元,请分别求出甲、乙两人的每月应缴纳的个人所得税;
(2)若丙每月缴纳的个人所得税为85元,则丙每月的工资收入额应为多少?
一、以个人每月工资收入额减去 3500元后的余额作为其每月应纳税所得额;
二、个人所得税纳税税率如下表所示:
| 纳税级数 | 个人每月应纳税所得额 | 纳税税率 |
| 1 | 不超过1500元的部分 | 3% |
| 2 | 超过1500元至4500元的部分 | 10% |
| 3 | 超过4500元至9000元的部分 | 20% |
| 4 | 超过9000元至35000元的部分 | 25% |
| 5 | 超过35000元至55000元的部分 | 30% |
| 6 | 超过55000元至80000元的部分 | 35% |
| 7 | 超过80000元的部分 | 45% |
(2)若丙每月缴纳的个人所得税为85元,则丙每月的工资收入额应为多少?
17.下列一组数:8,-2.6,-3$\frac{1}{2}$,2$\frac{2}{3}$,-5.7中负分数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
14.下列说法正确的是( )
| A. | 任何两个互为相反数的数的商为-1 | |
| B. | 任何一个不是1的正数都大于它的倒数 | |
| C. | 若a>b>0,则$\frac{1}{a}>\frac{1}{b}$ | |
| D. | 若$\frac{1}{a}<-1$,则-1<a<0 |
 如图所示,已知△ABE≌△ACD,指出它们的对应边和对应角.
如图所示,已知△ABE≌△ACD,指出它们的对应边和对应角.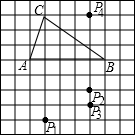 如图,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,从P1,P2,P3,P4四个点中找出符合条件的点P,则点P的个数为( )
如图,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,从P1,P2,P3,P4四个点中找出符合条件的点P,则点P的个数为( )