题目内容
9.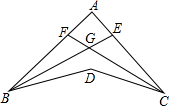 如图,BE平分∠ABD,CF平分∠ACD,BE、CF交于G,若∠BDC=150°,∠BGC=120°,求∠A的度数.
如图,BE平分∠ABD,CF平分∠ACD,BE、CF交于G,若∠BDC=150°,∠BGC=120°,求∠A的度数.
分析 根据三角形的内角和定理,及角平分线上的性质先计算∠ABC+∠ACB的度数,从而得出∠A的度数
解答 解:如图,连接BC.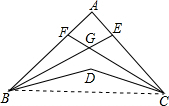
∵BE是∠ABD的平分线,CF是∠ACD的平分线,
∴∠ABE=∠DBE=$\frac{1}{2}$∠ABD,∠ACF=∠DCF=$\frac{1}{2}$∠ACD,
又∠BDC=150°,∠BGC=120°,
∴∠DBC+∠DCB=30°,∠GBC+∠GCB=60°,
∴∠EBD+∠FCD=60°-30°=30°,
∴∠ABE+∠ACF=30°,
∴∠ABE+∠ACF+∠GBC+∠GCB=60°+30°=90°,即∠ABC+∠ACB=90°,
∴∠A=90°.
点评 本题考查角平分线的性质及三角形的内角和定理,根据题意作出辅助线,构造出三角形是解答此题的关键

练习册系列答案
相关题目
19. 把一副直角三角板ABC(含30°、60°角)和CDE(含45°、45°角)如图放置,使直角顶点C重合,若DE∥BC,则∠1的度数是( )
把一副直角三角板ABC(含30°、60°角)和CDE(含45°、45°角)如图放置,使直角顶点C重合,若DE∥BC,则∠1的度数是( )
 把一副直角三角板ABC(含30°、60°角)和CDE(含45°、45°角)如图放置,使直角顶点C重合,若DE∥BC,则∠1的度数是( )
把一副直角三角板ABC(含30°、60°角)和CDE(含45°、45°角)如图放置,使直角顶点C重合,若DE∥BC,则∠1的度数是( )| A. | 75° | B. | 105° | C. | 110° | D. | 120° |
14.下列运算正确的是( )
| A. | a•a2=a2 | B. | a2+a2=a4 | C. | a6÷a2=a3 | D. | (2a)2=4a2 |
18.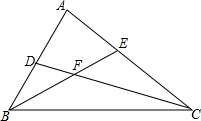 在△ABC中,如图,CD平分∠ACB,BE平分∠ABC,CD与BE交于点F,若∠DFE=120°,则∠A=( )
在△ABC中,如图,CD平分∠ACB,BE平分∠ABC,CD与BE交于点F,若∠DFE=120°,则∠A=( )
 在△ABC中,如图,CD平分∠ACB,BE平分∠ABC,CD与BE交于点F,若∠DFE=120°,则∠A=( )
在△ABC中,如图,CD平分∠ACB,BE平分∠ABC,CD与BE交于点F,若∠DFE=120°,则∠A=( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
19.如果半径为3cm的⊙O1与半径为4cm的⊙O2外切,那么两圆的圆心距是( )
| A. | 1cm | B. | 7cm | ||
| C. | 1cm或7cm | D. | 大于1cm且小于7cm |
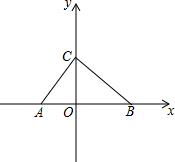 如图所示,点A、B、C的坐标分别为(-$\sqrt{2}$,0),(2$\sqrt{2}$,0),(0,2).
如图所示,点A、B、C的坐标分别为(-$\sqrt{2}$,0),(2$\sqrt{2}$,0),(0,2).