题目内容
如图,四边形ABCD中,∠ABC+∠D=180°,AC平分∠BAD,,E是AB延长线上一点,且CE⊥AE, CF⊥AD,
CF⊥AD,
试说明:(1)△CBE≌△CDF;
(2)AB+AD=2AF.
(1) ∵AC平分∠BAD,CE⊥AE,CF⊥AD
∴ CE=CF………………………………….1分
∵ ∠ABC+∠CBE=180º
∠ABC+∠D=180°
 ∴∠CBE=∠D ………………3分
∴∠CBE=∠D ………………3分
在 △CBE 和△CDF中
∠CBE=∠D
∠BEC=∠CFD
CE=CD
△CBE≌△CDF(AAS) ………………6分
(2) ∵由(1) △CBE≌△CDF(AAS)
∴BE=DF
在 △AEC 和△AFC中
CE=CF
AC=AC
∠AEC=∠AFC
△AEC ≌△AFC(HL) ………………9分
∴AE=AF
∴AB+AD=AE+AF
∴AB+AD=2AF ………………12分

练习册系列答案
 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
如图,二次函数y=ax2+bx+c的图象开口向上,对称轴为直线x=1,图象经过(3,0),下列结论中,正确的一项是( )(原创)
|
| A.2a+b | <0 | B. | 3a+c<0 | C. | a+b+c>0 | D. | 4ac﹣b2<0 |
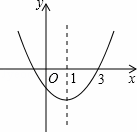
 位置,A点落在
位置,A点落在 位置,若
位置,若 ,则
,则 的度数是…( )
的度数是…( )
 ,点
,点 分别在射线
分别在射线 上运动,
上运动, 平分
平分 ,
, 的平分线交于点
的平分线交于点 .当
.当 时,则
时,则 的度数是
的度数是  B、
B、  C、
C、  D、
D、

 ,求代数式
,求代数式 的值。
的值。 B、
B、 C、
C、 D、
D、

 ____时,分式
____时,分式 有意义。
有意义。 ,求分式
,求分式 的值
的值