题目内容
18.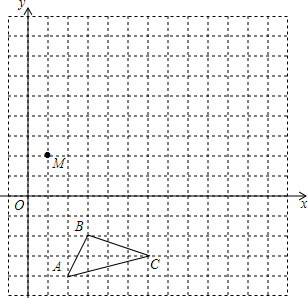 在平面直角坐标系中,△ABC的三个顶点坐标分别为A(2,-4),B(3,-2),C(6,-3).
在平面直角坐标系中,△ABC的三个顶点坐标分别为A(2,-4),B(3,-2),C(6,-3).(1)画出△ABC关于x轴对称的△A1B1C1;
(2)以M点为位似中心,在网格中画出△A1B1C1的位似图形△A2B2C2,使△A2B2C2与△A1B1C1的相似比为2:1;
(3)若每一个方格的面积为1,则△A2B2C2的面积为14.
分析 (1)直接利用关于x轴对称点的性质得出对应点位置进而得出答案;
(2)利用位似图形的性质得出对应点位置进而得出答案;
(3)利用△A2B2C2所在矩形的面积减去周围三角形面积进而得出答案.
解答  解:(1)如图所示:△A1B1C1,即为所求;
解:(1)如图所示:△A1B1C1,即为所求;
(2)如图所示:△A2B2C2,即为所求;
(3)△A2B2C2的面积为:4×8-$\frac{1}{2}$×2×4-$\frac{1}{2}$×2×6-$\frac{1}{2}$×2×8=14.
故答案为:14.
点评 此题主要考查了轴对称变换和位似变换以及三角形面积求法,根据题意得出对应点位置是解题关键.

练习册系列答案
相关题目
 如图,△ABC中,∠C=90°,DE是AB的垂直平分线,且∠BAD:∠CAD=1:1,求证:∠B=30°.
如图,△ABC中,∠C=90°,DE是AB的垂直平分线,且∠BAD:∠CAD=1:1,求证:∠B=30°.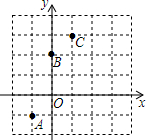 如图,已知二次函数y=ax2+bx+c的图象经过A(一1,-1),B(0,2),C(1,3).
如图,已知二次函数y=ax2+bx+c的图象经过A(一1,-1),B(0,2),C(1,3).