题目内容
17.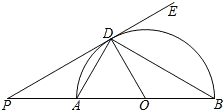 如图,AB是半圆的直径,O为圆心,AD、BD是半圆的弦,且∠PDA=∠PBD.判断直线PD是否为⊙O的切线,并说明理由.
如图,AB是半圆的直径,O为圆心,AD、BD是半圆的弦,且∠PDA=∠PBD.判断直线PD是否为⊙O的切线,并说明理由.
分析 根据圆周角定理,可得∠ADB的度数,根据等腰三角形的性质,可得∠OBD=∠ODB,根据余角的性质,可得∠ODA+∠PDA,根据切线的判定,可得答案.
解答 解:PD是⊙O的切线.理由如下:
∵AB为直径,
∵∠ADB=90°,
∴∠ADO+∠ODB=90°.
∵OD=OB,
∴∠OBD=∠ODB.
∵∠PDA=∠PBD,
∴∠ODA+∠PDA=90°.即∠PDO=90°,
又∵直线PD经过⊙O半径的外端,
∴PD是⊙O的切线.
点评 本题考查了切线的判定,利用余角的性质得出得∠ODA+∠PDA=90°是解题关键.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
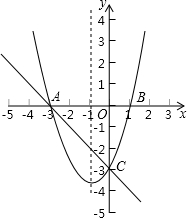 如图:抛物线y1=ax2+bx+c与直线y2=kx+b交于A(-3,0)、C(0,-3)两点,抛物线与x轴交于另一点B(1,0).利用图象填空:
如图:抛物线y1=ax2+bx+c与直线y2=kx+b交于A(-3,0)、C(0,-3)两点,抛物线与x轴交于另一点B(1,0).利用图象填空:
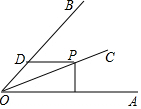 如图,OC平分∠AOB=60°,且∠AOB=60°,点P为OC上任意点,PM⊥OA于M,PD∥OA,交OB于D,若OM=6,则PD的长为( )
如图,OC平分∠AOB=60°,且∠AOB=60°,点P为OC上任意点,PM⊥OA于M,PD∥OA,交OB于D,若OM=6,则PD的长为( ) 在△ABC中,∠C=90°,BC=4cm,∠BAC的平分线交BC于D,且BD:DC=5:3,则D到AB的距离为1.5 cm.
在△ABC中,∠C=90°,BC=4cm,∠BAC的平分线交BC于D,且BD:DC=5:3,则D到AB的距离为1.5 cm.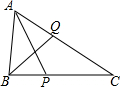 如图,在△ABC中,∠BAC=60°,∠C=40°,P,Q分别在BC,CA上,AP,BQ分别是∠BAC,∠ABC的角平分线.求证:BQ+AQ=AB+BP.
如图,在△ABC中,∠BAC=60°,∠C=40°,P,Q分别在BC,CA上,AP,BQ分别是∠BAC,∠ABC的角平分线.求证:BQ+AQ=AB+BP.