题目内容
16.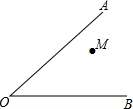 如图所示,M是∠AOB内-点.
如图所示,M是∠AOB内-点.(1)分别作出点M关于OA,0B的对称点M1,M2,联结M1M2,交OA于点P,交0B于Q.
(2)若M1M2=10cm,求△MPQ的周长.
(3)在OA、OB上任取点P′、Q′,联接MP′、P′Q′、MQ′,得到△MP′Q′.比较△MP′Q′与△MPQ的周长,你能得到什么结论?
分析 (1)利用关于直线对称点的图形的性质得出对应点位置进而得出答案;
(2)利用轴对称变换的性质得出对应线段之间的关系进而得出答案;
(3)利用(2)中所求得出△MPQ的周长面积最小,进而得出答案.
解答 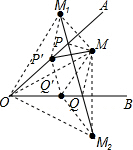 解:(1)如图所示:
解:(1)如图所示:
(2)∵点M关于OA,0B的对称点M1,M2,
∴M1P=PM,QM=QM2,
∴△MPQ的周长等于M1P+PQ+M2Q=M1M2=10cm;
(3)如图所示:由△MPQ的周长等于M1M2,则此时△MPQ的周长面积最小,
△MP′Q′的周长为:M1P′+P′Q′+Q′M2,
故△MP′Q′大于△MPQ的周长.
点评 此题主要考查了轴对称变换以及线段垂直平分线的性质,得出M1P=PM,QM=QM2是解题关键.

练习册系列答案
相关题目
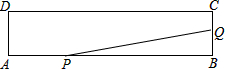 如图所示,矩形ABCD的两边长AB=18cm,AD=4cm,点P、Q分别从A、B同时出发,点P在边AB边上沿AB方向以2cm/s的速度匀速运动,点Q在边BC边上沿BC方向以1cm/s的速度匀速运动,当其中一个点停止运动时,另一个点也停止运动,设运动时间为xs,△PBQ的面积为y(cm2).
如图所示,矩形ABCD的两边长AB=18cm,AD=4cm,点P、Q分别从A、B同时出发,点P在边AB边上沿AB方向以2cm/s的速度匀速运动,点Q在边BC边上沿BC方向以1cm/s的速度匀速运动,当其中一个点停止运动时,另一个点也停止运动,设运动时间为xs,△PBQ的面积为y(cm2). 如图,点A,E,B,D在同一条直线上,AE=DB,∠A=∠D,∠C=∠F.试判断△ABC与△DEF是否全等,并说明理由.
如图,点A,E,B,D在同一条直线上,AE=DB,∠A=∠D,∠C=∠F.试判断△ABC与△DEF是否全等,并说明理由.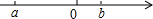 a,b在数轴上如图,则:
a,b在数轴上如图,则: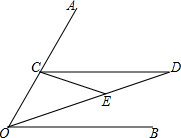 已知∠AOB,点C是OA上任意一点,CD∥OB,且∠AOE=∠CEO,∠DCE=∠D,试说明∠DOB=$\frac{1}{3}$∠AOB.
已知∠AOB,点C是OA上任意一点,CD∥OB,且∠AOE=∠CEO,∠DCE=∠D,试说明∠DOB=$\frac{1}{3}$∠AOB.