题目内容
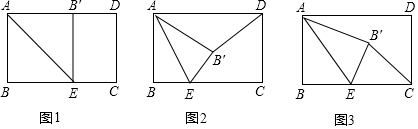
15．
如图，已知四边形ABCD是矩形，对角线AC、BD交于点O，CE∥BD，DE∥AC，CE与DE交于点E．求证：四边形OCED是菱形．
分析 先证明四边形OCED是平行四边形，再由矩形的性质得出OC=OD，证出四边形OCED是菱形即可．
解答 解：OE⊥DC，理由如下：
∵DE∥AC，CE∥BD，
∴四边形OCED是平行四边形，
∵四边形ABCD是矩形，
∴OC=$\frac{1}{2}$AC，OD=$\frac{1}{2}$BD，AC=BD，
∴OC=OD，
∴四边形OCED是菱形．
点评 本题考查了平行四边形的判定、矩形的性质、菱形的判定；熟练掌握矩形的性质和菱形的判定是解决问题的关键．
练习册系列答案
精英口算卡系列答案
应用题点拨系列答案
相关题目
如图，在菱形ABCD中，∠DAB=45°，AB=8，点P为线段AB上一动点，过点P作PE⊥AB交直线AD于E，沿PE将∠A折叠，点A的对称点为点F，连接EF、DF、GF，当△CDF为直角三角形时，AP=2$\sqrt{2}$或4+2$\sqrt{2}$．
6．
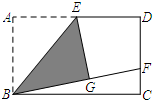如图，在矩形ABCD中，E是AD的中点，将△ABE沿BE折叠后得到△GBE，延长BG交CD于点F，连接EF，若AB=3，AD=4，则△BCF的周长为（ ）
如图，在矩形ABCD中，E是AD的中点，将△ABE沿BE折叠后得到△GBE，延长BG交CD于点F，连接EF，若AB=3，AD=4，则△BCF的周长为（ ）| A． | $\frac{13}{3}$ | B． | $\frac{25}{3}$ | C． | 10 | D． | 12 |
如图从一个建筑物的A处测得对面楼BC的顶部B的仰角为37°，底部C的俯角为45°，观察点与楼的水平距离AD为40m，求楼BC的高度（参考数据：sin37°≈0.60；cos37°≈0.80；tan37°≈0.75）
如图所示，课间操时，小华、小军、小刚的位置如图，小华对小刚说：“如果我的位置用（0，0）表示，小军的位置用（2，1）表示，那么你的位置应表示为（4，3）．”