题目内容
5. 如图,在菱形ABCD中,∠DAB=45°,AB=8,点P为线段AB上一动点,过点P作PE⊥AB交直线AD于E,沿PE将∠A折叠,点A的对称点为点F,连接EF、DF、GF,当△CDF为直角三角形时,AP=2$\sqrt{2}$或4+2$\sqrt{2}$.
如图,在菱形ABCD中,∠DAB=45°,AB=8,点P为线段AB上一动点,过点P作PE⊥AB交直线AD于E,沿PE将∠A折叠,点A的对称点为点F,连接EF、DF、GF,当△CDF为直角三角形时,AP=2$\sqrt{2}$或4+2$\sqrt{2}$.
分析 分两种情形①如图1,如图1,当DF⊥AB时,△CDF是直角三角形,②如图2,当CF⊥AB时,△DCF是直角三角形分别求出即可.
解答 解:如图1,当DF⊥AB时,△CDF是直角三角形,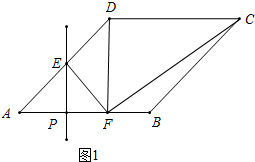
∵在菱形ABCD中,AB=8,
∴CD=AD=AB=4,
在Rt△ADF中,∵AD=8,∠DAN=45°DF=AF=4$\sqrt{2}$,
∴AP=$\frac{1}{2}$AF=2$\sqrt{2}$,
如图2,当CF⊥AB时,△DCF是直角三角形,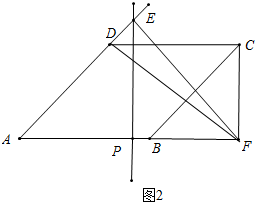
在Rt△CBF中,∵∠CFB=90°,∠CBF=∠A=45°,BC=8,
∴BF=CF=4$\sqrt{2}$,
∴AF=8+4$\sqrt{2}$,
∴AP=$\frac{1}{2}$AF=4+2$\sqrt{2}$.
故答案为:2$\sqrt{2}$或4+2$\sqrt{2}$.
点评 本题考查了菱形的性质,等腰直角三角形的性质,折叠的性质,熟练掌握折叠的性质是解题的关键,学会正确画出图象,注意分类讨论的思想,属于中考常考题型.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
10.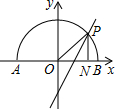 如图,半径为1的半圆的圆心在原点,直径AB在x轴上,过原点的任意一条半径与半圆交于点P,过P作PN垂直于x轴,N为垂足,则∠OPN的平分线过定点( )
如图,半径为1的半圆的圆心在原点,直径AB在x轴上,过原点的任意一条半径与半圆交于点P,过P作PN垂直于x轴,N为垂足,则∠OPN的平分线过定点( )
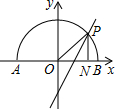 如图,半径为1的半圆的圆心在原点,直径AB在x轴上,过原点的任意一条半径与半圆交于点P,过P作PN垂直于x轴,N为垂足,则∠OPN的平分线过定点( )
如图,半径为1的半圆的圆心在原点,直径AB在x轴上,过原点的任意一条半径与半圆交于点P,过P作PN垂直于x轴,N为垂足,则∠OPN的平分线过定点( )| A. | (0,-1) | B. | (0,-$\frac{4}{5}$) | C. | (0,-$\frac{3}{5}$) | D. | (0,-$\frac{6}{5}$) |
14.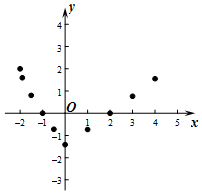 有这样一个问题:探究函数y=-$\sqrt{x+2}$+|x|的图象与性质.?
有这样一个问题:探究函数y=-$\sqrt{x+2}$+|x|的图象与性质.?
小军根据学习函数的经验,对函数y=-$\sqrt{x+2}$+|x|的图象与性质进行了探究.
下面是小军的探究过程,请补充完整:
(1)函数y=-$\sqrt{x+2}$+|x|的自变量x的取值范围是x≥-2;
(2)表是y与x的几组对应值?
在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(3)观察图象,函数的最小值是-$\sqrt{2}$;
(4)进一步探究,结合函数的图象,写出该函数的一条性质(函数最小值除外):当-2≤x<0时,y随x的增大而减小.
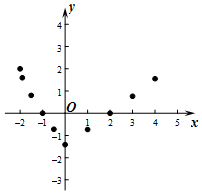 有这样一个问题:探究函数y=-$\sqrt{x+2}$+|x|的图象与性质.?
有这样一个问题:探究函数y=-$\sqrt{x+2}$+|x|的图象与性质.?小军根据学习函数的经验,对函数y=-$\sqrt{x+2}$+|x|的图象与性质进行了探究.
下面是小军的探究过程,请补充完整:
(1)函数y=-$\sqrt{x+2}$+|x|的自变量x的取值范围是x≥-2;
(2)表是y与x的几组对应值?
| x | -2 | -1.9 | -1.5 | -1 | -0.5 | 0 | 1 | 2 | 3 | 4 | … |
| y | 2 | 1.60 | 0.80 | 0 | -0.72 | -1.41 | -0.37 | 0 | 0.76 | 1.55 | … |
(3)观察图象,函数的最小值是-$\sqrt{2}$;
(4)进一步探究,结合函数的图象,写出该函数的一条性质(函数最小值除外):当-2≤x<0时,y随x的增大而减小.
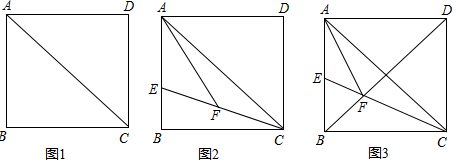

 如图,已知四边形ABCD是矩形,对角线AC、BD交于点O,CE∥BD,DE∥AC,CE与DE交于点E.
如图,已知四边形ABCD是矩形,对角线AC、BD交于点O,CE∥BD,DE∥AC,CE与DE交于点E.