题目内容
2.先化简,再求值:(a+1-$\frac{4a-5}{a-1}$)÷($\frac{1}{a}$-$\frac{1}{{a}^{2}-a}$),其中a=2+$\sqrt{3}$.分析 原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,把a的值代入计算即可求出值.
解答 解:原式=$\frac{{a}^{2}-1-4a+5}{a-1}$÷$\frac{a-1-1}{a(a-1)}$=$\frac{(a-2)^{2}}{a-1}$•$\frac{a(a-1)}{a-2}$=a(a-2)=a2-2a,
当a=2+$\sqrt{3}$时,原式=7+4$\sqrt{3}$-4-2$\sqrt{3}$=3-2$\sqrt{3}$.
点评 此题考查了分式的化简求值,以及分式的值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
12.下列图形中,既是轴对称图形,又是中心对称图形的是( )
| A. | 等边三角形 | B. | 平行四边形 | C. | 等腰三角形 | D. | 正六边形 |
13.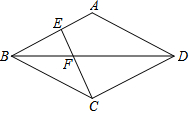 如图,菱形ABCD中,BD为ABCD的对角线,且CE⊥AB,交BD于点F,BD=8,AB=5,则CE的值是( )
如图,菱形ABCD中,BD为ABCD的对角线,且CE⊥AB,交BD于点F,BD=8,AB=5,则CE的值是( )
 如图,菱形ABCD中,BD为ABCD的对角线,且CE⊥AB,交BD于点F,BD=8,AB=5,则CE的值是( )
如图,菱形ABCD中,BD为ABCD的对角线,且CE⊥AB,交BD于点F,BD=8,AB=5,则CE的值是( )| A. | $\frac{12}{5}$ | B. | $\frac{24}{5}$ | C. | $\frac{48}{5}$ | D. | $\frac{8}{5}$ |
 如图,矩形ABCD的边AB过⊙O的圆心,E、F分别为AB、CD与⊙O的交点,若AE=3cm,AD=4cm,DF=5cm,求⊙O的直径.
如图,矩形ABCD的边AB过⊙O的圆心,E、F分别为AB、CD与⊙O的交点,若AE=3cm,AD=4cm,DF=5cm,求⊙O的直径.