题目内容
 已知:如图,在△ABC中,点D是BC中点,点E是AC中点,且AD⊥BC,BE⊥AC,BE,AD相交于点G,过点B作BF∥AC交AD的延长线于点F,DF=6.
已知:如图,在△ABC中,点D是BC中点,点E是AC中点,且AD⊥BC,BE⊥AC,BE,AD相交于点G,过点B作BF∥AC交AD的延长线于点F,DF=6.(1)求AE的长;
(2)求
| S△AEG |
| S△FBG |
考点:相似三角形的判定与性质,等边三角形的判定与性质
专题:
分析:(1)根据等边三角形的性质和判定推出∠C=60°,求出∠CBF=60°,∠F=30°,解直角三角形求出BD,即可得出答案;
(2)求出BF长,根据相似三角形的性质和判定得出即可.
(2)求出BF长,根据相似三角形的性质和判定得出即可.
解答:解:(1)∵在△ABC中,点D是BC中点,点E是AC中点,且AD⊥BC,BE⊥AC,
∴AC=AB=BC,
∴△ABC是等边三角形,
∴∠C=60°,
∵BF∥AC,
∴∠CBF=∠C=60°,
∵AD⊥BC,
∴∠FDB=90°,
∴∠F=30°,
∵DF=6,
∴BD=2
,
∵AE=EC=BD=DC,
∴AE=2
;
(2)∵∠BDF=90°,∠F=30°,BD=2
,
∴BF=2DB=4
,
∵AC∥BF,
∴△AEG∽△FBG,
∴
=(
)2=
.
∴AC=AB=BC,
∴△ABC是等边三角形,
∴∠C=60°,
∵BF∥AC,
∴∠CBF=∠C=60°,
∵AD⊥BC,
∴∠FDB=90°,
∴∠F=30°,
∵DF=6,
∴BD=2
| 3 |
∵AE=EC=BD=DC,
∴AE=2
| 3 |
(2)∵∠BDF=90°,∠F=30°,BD=2
| 3 |
∴BF=2DB=4
| 3 |
∵AC∥BF,
∴△AEG∽△FBG,
∴
| S△AEG |
| S△FBG |
| AE |
| BF |
| 1 |
| 4 |
点评:本题考查了含30度角的直角三角形性质,勾股定理,解直角三角形,平行线的性质,相似三角形的性质和判定的应用,注意:相似三角形的面积比等于相似比的平方.

练习册系列答案
相关题目
下列语句不是命题的是( )
| A、画两个相等的角 |
| B、2是一个偶数 |
| C、等边三角形是特殊的等腰三角形 |
| D、直角小于锐角 |
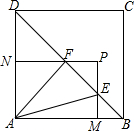 如图,正方形ABCD的边长为2,P是△BCD内一动点,过点P作PM⊥AB于M,PN⊥AD于N,分别于对角线BD相交于点E,F.记PM=a,PN=b,当点P运动时,ab=2.
如图,正方形ABCD的边长为2,P是△BCD内一动点,过点P作PM⊥AB于M,PN⊥AD于N,分别于对角线BD相交于点E,F.记PM=a,PN=b,当点P运动时,ab=2. 当a=
当a=