题目内容
一服装厂的工资标准为:“本厂工人只需每天工作8小时,每月工作25天,就可享受1200元/月的出勤工资.再加计件工资,多劳多得”.下表是女工丁晓芬记录的两个时间段加工上衣、裤子的数量,所用时间和结算的计件工资数据:
(1)根据表格中的信息,分别求出丁晓芬加工1件上衣、1条裤子所需的时间;
(2)根据表格中的信息,假设丁晓芬的工作效率不变,分别求出她加工1件上衣、1条裤子可得到的计件工资数;
(3)假设丁晓芬的工作效率不变,在某个月出满勤(工作了25天,每天工作了8小时),若工厂规定加工裤子的时间不得少于加工上衣的时间.求她这个月的月工资y(计件工资+出勤工资=月工资)最多为多少元?
| 上衣(件) | 裤子(条) | 总时间(分钟) | 总计件工资(元) |
| 6 | 5 | 488 | 44.8 |
| 3 | 8 | 464 | 40 |
(2)根据表格中的信息,假设丁晓芬的工作效率不变,分别求出她加工1件上衣、1条裤子可得到的计件工资数;
(3)假设丁晓芬的工作效率不变,在某个月出满勤(工作了25天,每天工作了8小时),若工厂规定加工裤子的时间不得少于加工上衣的时间.求她这个月的月工资y(计件工资+出勤工资=月工资)最多为多少元?
考点:一次函数的应用,二元一次方程组的应用
专题:
分析:(1)设丁晓芬加工1件上衣需要的时间为x分钟,加工1条裤子所需的时间为y分钟,根据条件建立方程组求出其解即可;
(2)设丁晓芬加工1件上衣所得的工资是a元,加工1条裤子所得的工资是b元,根据条件建立方程组求出其解即可;
(3)设加工上衣的时间是m分钟,则加工裤子的时间是(25×8×60-m)分钟,根据计件工资+出勤工资=月工资和工厂规定加工裤子的时间不得少于加工上衣的时间建立不等式组,求出其y与m的关系式,根据一次函数的性质就可以求出结论.
(2)设丁晓芬加工1件上衣所得的工资是a元,加工1条裤子所得的工资是b元,根据条件建立方程组求出其解即可;
(3)设加工上衣的时间是m分钟,则加工裤子的时间是(25×8×60-m)分钟,根据计件工资+出勤工资=月工资和工厂规定加工裤子的时间不得少于加工上衣的时间建立不等式组,求出其y与m的关系式,根据一次函数的性质就可以求出结论.
解答:解:(1)设丁晓芬加工1件上衣需要的时间为x分钟,加工1条裤子所需的时间为y分钟,由题意,得
,
解得:
.
答:丁晓芬加工1件上衣需要的时间为48分钟,加工1条裤子所需的时间为40分钟;
(2)设丁晓芬加工1件上衣所得的工资是a元,加工1条裤子所得的工资是b元,由题意,得
,
解得:
,
答:丁晓芬加工1件上衣所得的工资是4.8元,加工1条裤子所得的工资是3.2元;
(3)设加工上衣的时间是m分钟,则加工裤子的时间是(25×8×60-m)分钟,由题意,得
,
解得:m≤6000.
y=
m+2160.
∴k=
>0,
∴y随m的增大而增大,
∴当m=6000时,
y最大=2280.
答:她这个月的月工资最多为2280元.
|
解得:
|
答:丁晓芬加工1件上衣需要的时间为48分钟,加工1条裤子所需的时间为40分钟;
(2)设丁晓芬加工1件上衣所得的工资是a元,加工1条裤子所得的工资是b元,由题意,得
|
解得:
|
答:丁晓芬加工1件上衣所得的工资是4.8元,加工1条裤子所得的工资是3.2元;
(3)设加工上衣的时间是m分钟,则加工裤子的时间是(25×8×60-m)分钟,由题意,得
|
解得:m≤6000.
y=
| 1 |
| 50 |
∴k=
| 1 |
| 50 |
∴y随m的增大而增大,
∴当m=6000时,
y最大=2280.
答:她这个月的月工资最多为2280元.
点评:本题考查了一次函数的解析式的运用,二元一次方程组的解法的运用,解答时根据题意的数量关系建立方程组时关键,求出一次函数的解析式是难点.

练习册系列答案
相关题目
 力龙羽毛球商场经理对新进某一品牌几种号码的男式羽毛球鞋的销售情况进行了一周的统计,得到一组数据后,绘制了频数、频率统计表与频数分布直方图如图所示:
力龙羽毛球商场经理对新进某一品牌几种号码的男式羽毛球鞋的销售情况进行了一周的统计,得到一组数据后,绘制了频数、频率统计表与频数分布直方图如图所示:
 已知:如图,在△ABC中,点D是BC中点,点E是AC中点,且AD⊥BC,BE⊥AC,BE,AD相交于点G,过点B作BF∥AC交AD的延长线于点F,DF=6.
已知:如图,在△ABC中,点D是BC中点,点E是AC中点,且AD⊥BC,BE⊥AC,BE,AD相交于点G,过点B作BF∥AC交AD的延长线于点F,DF=6.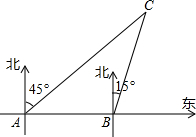 钓鱼岛自古以来就是我国的神圣领土,为维护国家主权和海洋权利,我国海监和渔政部门对钓鱼岛海域实现了常态化巡航管理.如图,某日在我国钓鱼岛附近海域有两艘自西向东航行的海监船A、B,B船在A船的正东方向,且两船保持40海里的距离,某一时刻两海监船同时测得在A的东北方向,B的北偏东15°方向有一我国渔政执法船C.
钓鱼岛自古以来就是我国的神圣领土,为维护国家主权和海洋权利,我国海监和渔政部门对钓鱼岛海域实现了常态化巡航管理.如图,某日在我国钓鱼岛附近海域有两艘自西向东航行的海监船A、B,B船在A船的正东方向,且两船保持40海里的距离,某一时刻两海监船同时测得在A的东北方向,B的北偏东15°方向有一我国渔政执法船C.