题目内容
1.(1)解方程:$\frac{1}{x-1}$-$\frac{3}{{x}^{2}-1}$=0(2)求不等式组$\left\{\begin{array}{l}{x-3(x-2)≥4}\\{\frac{1+4x}{3}>x-1}\end{array}\right.$的整数解.
分析 (1)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解;
(2)分别求出不等式组中两不等式的解集,找出解集的公共部分确定出不等式组的解集,即可求出不等式组的整数解.
解答 解:(1)去分母得:x+1-3=0,
解得:x=2,
经检验x=2是分式方程的解;
(2)$\left\{\begin{array}{l}{x-3(x-2)≥4①}\\{\frac{1+4x}{3}>x-1②}\end{array}\right.$,
由①得:x≤1,
由②得:x>-4,
∴不等式组的解集为-4<x≤1,
则不等式组的整数解为-3,-2,-1,0,1.
点评 此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
相关题目
9.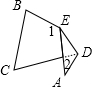 如图:把△ABC纸片沿DE折叠,当点A在四边形BCDE的外部时,记∠AEB为∠1,∠ADC为∠2,则∠A、∠1与∠2的数量关系,结论正确的是( )
如图:把△ABC纸片沿DE折叠,当点A在四边形BCDE的外部时,记∠AEB为∠1,∠ADC为∠2,则∠A、∠1与∠2的数量关系,结论正确的是( )
 如图:把△ABC纸片沿DE折叠,当点A在四边形BCDE的外部时,记∠AEB为∠1,∠ADC为∠2,则∠A、∠1与∠2的数量关系,结论正确的是( )
如图:把△ABC纸片沿DE折叠,当点A在四边形BCDE的外部时,记∠AEB为∠1,∠ADC为∠2,则∠A、∠1与∠2的数量关系,结论正确的是( )| A. | ∠1=∠2+∠A | B. | ∠1=2∠A+∠2 | C. | ∠1=2∠2+2∠A | D. | 2∠1=∠2+∠A |
13. 如图,小半圆的直径与大半圆的直径AB重合,圆心重合,弦CD与小半圆相切,CD=10,则阴影部分面积为( )
如图,小半圆的直径与大半圆的直径AB重合,圆心重合,弦CD与小半圆相切,CD=10,则阴影部分面积为( )
 如图,小半圆的直径与大半圆的直径AB重合,圆心重合,弦CD与小半圆相切,CD=10,则阴影部分面积为( )
如图,小半圆的直径与大半圆的直径AB重合,圆心重合,弦CD与小半圆相切,CD=10,则阴影部分面积为( )| A. | 100π | B. | 50π | C. | 25π | D. | 12.5π |
11.下列关于“1”的说法中,错误的是( )
| A. | 1的绝对值是1 | B. | 1的倒数是1 | C. | 1的相反数是1 | D. | 1是最小的正整数 |
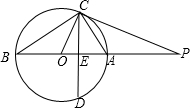 如图,AB是⊙O的直径,点P在BA的延长线上,点A是$\widehat{CD}$的中点,∠POC=∠PCE.
如图,AB是⊙O的直径,点P在BA的延长线上,点A是$\widehat{CD}$的中点,∠POC=∠PCE.
 为迎接“六一儿童节”,小天使培训班准备购买“悠悠兔卷笔刀”作为节日礼物送给小朋友.经调查发现:在“丽水沃尔玛超市”悠悠兔卷笔刀的单价为4元/个;在淘宝网店购买,同牌子卷笔刀的价格是超市的8.5折,但需快递费15元.
为迎接“六一儿童节”,小天使培训班准备购买“悠悠兔卷笔刀”作为节日礼物送给小朋友.经调查发现:在“丽水沃尔玛超市”悠悠兔卷笔刀的单价为4元/个;在淘宝网店购买,同牌子卷笔刀的价格是超市的8.5折,但需快递费15元.