题目内容
18．
如图，一只蚂蚁从长、宽、高都是3cm的正方体纸箱的A点沿纸箱爬到B点，那么它所走的最短路线的长是3$\sqrt{5}$．
分析 先将图形展开，再根据勾股定理求出AB的长即可．
解答 
解：如图所示：将正方体展开，
∵正方体的边长为2，
∴AC=6，BC=3，
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{6}^{2}+{3}^{2}}$=3$\sqrt{5}$．
故答案为：3$\sqrt{5}$．
点评 本题考查的是平面展开-最短路线问题，本题是一道趣味题，将正方体展开，运用勾股定理解答即可．
练习册系列答案
智慧小复习系列答案
相关题目
如图，FB⊥AB，EC⊥AB，∠1=∠D=45°，则图中与∠CED相等的角共有4个．
13．在实数-3.14，$-\sqrt{2}$，0.1010010001，$-\frac{π}{3}$，$\frac{1}{7}$，$\sqrt{4}$中，无理数有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
3．在平面直角坐标系中，点A坐标为（4，5），点A向左平移5个单位长度到点A1，则点A1的坐标是（ ）
| A． | （-1，5） | B． | （0，5） | C． | （9，5） | D． | （-1，0） |
7．
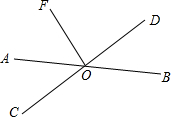如图，直线AB、CD相交于点O，OF⊥CO，∠AOF与∠BOD的度数之比为3：2，则∠AOC的度数是（ ）
如图，直线AB、CD相交于点O，OF⊥CO，∠AOF与∠BOD的度数之比为3：2，则∠AOC的度数是（ ）| A． | 18° | B． | 45° | C． | 36° | D． | 30° |
如图，△ABC中，∠C=90°，∠A=30°，AB的垂直平分线交AC于D，交AB于E，CD=2，则AC等于（ ）