题目内容
已知等边△ABC的边长为3个单位,若点P由A出发,以每秒1个单位的速度在三角形的边上沿A B
B C
C A方向运动,第一次回到点A处停止运动,设AP=S,用
A方向运动,第一次回到点A处停止运动,设AP=S,用 表示运动时间.
表示运动时间.
(1)当点P由B到C运动的过程中,用 表示S;
表示S;
(2)当 取何值时,S等于
取何值时,S等于 (求出所有的
(求出所有的 值);
值);
(3)根据(2)中 的取值,直接写出在哪些时段AP
的取值,直接写出在哪些时段AP ?
?

【答案】
(1)S= 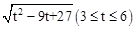 (2)
(2)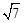 或4或5或9-
或4或5或9-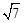 秒(3)
秒(3)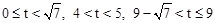
【解析】解:(1)如图,
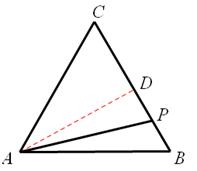
过点A作BC的高,则
∵等边△ABC的边长为3个单位
∴AB=BC=3,BD=CD=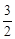 ,AD=
,AD= 。
。
又∵点P的运动速度是每秒1个单位,
∴BP=t﹣3,DP=∣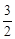 -(t﹣3)∣=∣
-(t﹣3)∣=∣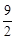 -t∣。
-t∣。
∴在Rt△APD中,根据勾股定理得
S=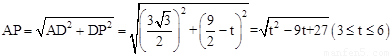 。
。
(2)当点P在AB上时,S=AP=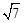 ,
,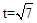 。
。
当点P在BC上时,由S=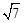 得t2﹣9t+27=7,解得t1=4,t2=5。
得t2﹣9t+27=7,解得t1=4,t2=5。
当点P在CA上时,S=AP=9-t=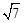 ,解得t=9-
,解得t=9-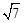 。
。
综上所述,当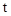 为
为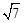 或4或5或9-
或4或5或9-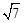 秒时,S等于
秒时,S等于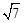 。
。
(3)由(2)得当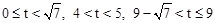 时,AP
时,AP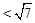 。
。
(1)过点A作BC的高,根据等边三角形的性质,求得BD和AD的长,用t表示出DP的长,在Rt△APD应用勾股定理即可表示出AP的长。
(2)分点P在AB上、点P在BC上和点P在CA上三种情况讨论即可。
(3)由(2)的三种情况分别写出即可。

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
 11、如图,已知等边△ABC的边长为8,P是△ABC内一点,PD∥AC,PE∥AD,PF∥BC,点D,E,F分别在AB,BC,AC上,则PD+PE+PF=
11、如图,已知等边△ABC的边长为8,P是△ABC内一点,PD∥AC,PE∥AD,PF∥BC,点D,E,F分别在AB,BC,AC上,则PD+PE+PF=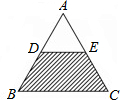 (2011•辽阳)如图,已知等边△ABC的面积为1,D、E分别为AB、AC的中点,若向图中随机抛掷一枚飞镖,飞镖落在阴影区域的概率是(不考虑落在线上的情形)( )
(2011•辽阳)如图,已知等边△ABC的面积为1,D、E分别为AB、AC的中点,若向图中随机抛掷一枚飞镖,飞镖落在阴影区域的概率是(不考虑落在线上的情形)( ) 动,第一次回到点A处停止运动,设AP=S,用t表示运动时间.
动,第一次回到点A处停止运动,设AP=S,用t表示运动时间.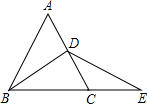 如图,已知等边△ABC的边长为2,BD是AC边上的中线,E为BC延长线上一点,且CD=CE,则DE=
如图,已知等边△ABC的边长为2,BD是AC边上的中线,E为BC延长线上一点,且CD=CE,则DE= 如图,已知等边△ABC的边长2,AD平分∠BAC.
如图,已知等边△ABC的边长2,AD平分∠BAC.