题目内容
11、如图，已知等边△ABC的边长为8，P是△ABC内一点，PD∥AC，PE∥AD，PF∥BC，点D，E，F分别在AB，BC，AC上，则PD+PE+PF=8
．分析：作辅助线，根据平行四边形的判定和性质及等腰三角形的性质，可证PD+PE+PF=AB=8．
解答：
解：过E点作EG∥PD，过D点作DH∥PF，
∵PD∥AC，EG∥PD，
∴四边形DGEP为平行四边形，
∴EG=DP，PE=GD，
又△ABC是等边三角形，EG∥AC，
△BEG为等边三角形，
∴EG=PD=GB，
同理可证：DH=PF=AD，
∴PD+PE+PF=BG+GD+AD=AB=8．
解：过E点作EG∥PD，过D点作DH∥PF，∵PD∥AC，EG∥PD，
∴四边形DGEP为平行四边形，
∴EG=DP，PE=GD，
又△ABC是等边三角形，EG∥AC，
△BEG为等边三角形，
∴EG=PD=GB，
同理可证：DH=PF=AD，
∴PD+PE+PF=BG+GD+AD=AB=8．
点评：此题主要考查平行四边形的判定和性质及等腰三角形的性质．熟练掌握性质定理和判定定理是解题的关键．
练习册系列答案
相关题目
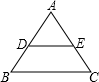
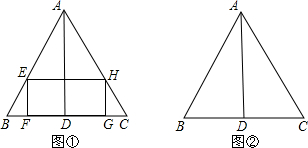
（2013•黄浦区二模）如图，已知等边△ABC的边长为1，设
如图，已知等边三角形ABC的边长为10，点P、Q分别为边AB、AC上的一个动点，点P从点B出发以1cm/s的速度向点A运动，点Q从点C出发以2cm/s的速度向点A运动，连接PQ，以Q为旋转中心，将线段PQ按逆时针方向旋转60°得线段QD，若点P、Q同时出发，则当运动