题目内容

如图，已知等边△ABC的边长2，AD平分∠BAC．
（1）求BD的长；
（2）求△ABC的面积．
分析：（1）利用三线合一定理即可求解；
（2）利用勾股定理即可求得AD的长，然后利用三角形的面积公式即可求解．
解答：解：（1）∵等边△ABC的边长2，AD平分∠BAC，
∴AD⊥BC，且BD=
1
2
BC=1；

（2）在直角△ABD中，AD=
AB2-BD2
=
3
，
则S△ABC=
1
2
BC•AD=
1
2
×2×
3
=
3
．
点评：本题考查了三线合一定理，以及三角形的面积公式，理解三线合一定理是关键．
练习册系列答案
相关题目
如图，已知等边三角形ABC的中位线DE的长为1，
则下面结论中正确的是
 
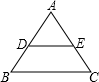
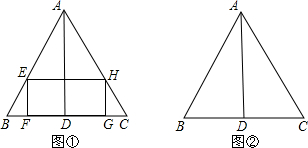
．（填序号）精英家教网
①AB=2；②△DAE≌△BAC；
③△DAE的周长与△BAC的周长之比为1：3；
④△DAE的面积与△BAC的面积之比为1：4．
如图，已知等边三角形ABC的边长为2，AD是BC边上的高．
（1）在△ABC内部作一个矩形EFGH（如图①），其中E、H分别在边AB、AC上，FG在边BC上．
①设矩形的一边FG=x，那么EF=
 
；（用含有x的代数式表示）精英家教网
②设矩形的面积为y，当x取何值时，y的值最大，最大值是多少？
（2）当矩形EFGH面积最大时，请在图②中画出此时点E的位置．（要求尺规作图，保留作图痕迹，并简要说明确定点E的方法）
（2013•黄浦区二模）如图，已知等边△ABC的边长为1，设
n
=
AB
+
BC
，那么向量
n
的模|
n
|=
1
1
．
（2007•临夏州）[（1）-（3），10分]如图，已知等边△ABC和点P，设点P到△ABC三边AB、AC、BC（或其延长线）的距离分别为h1、h2、h3，△ABC的高为h．
在图（1）中，点P是边BC的中点，此时h3=0，可得结论：h1+h2+h3=h．
在图（2）--（5）中，点P分别在线段MC上、MC延长线上、△ABC内、△ABC外．
（1）请探究：图（2）--（5）中，h1、h2、h3、h之间的关系；（直接写出结论）
（2）证明图（2）所得结论；
（3）证明图（4）所得结论．
（4）在图（6）中，若四边形RBCS是等腰梯形，∠B=∠C=60°，RS=n，BC=m，点P在梯形内，且点P到四边BR、RS、SC、CB的距离分别是h1、h2、h3、h4，桥形的高为h，则h1、h2、h3、h4、h之间的关系为：
m（h1+h2+h3）-n（h1+h3-h4）=（m+n）h
m（h1+h2+h3）-n（h1+h3-h4）=（m+n）h
；图（4）与图（6）中的等式有何关系？
如图，已知等边三角形ABC的边长为10，点P、Q分别为边AB、AC上的一个动点，点P从点B出发以1cm/s的速度向点A运动，点Q从点C出发以2cm/s的速度向点A运动，连接PQ，以Q为旋转中心，将线段PQ按逆时针方向旋转60°得线段QD，若点P、Q同时出发，则当运动
10
3
10
3
s时，点D恰好落在BC边上．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网