题目内容
6.解方程:(1)$\frac{x+2}{x}=1-\frac{x-5}{3}$
(2)$\left\{\begin{array}{l}{y=2x-7}\\{3x+y=8}\end{array}\right.$.
分析 (1)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解;
(2)方程组利用代入消元法求出解即可.
解答 解:(1)去分母得:3x+6=3x-x2+5x,
解得:x=2或x=3,
经检验x=2与x=3都是分式方程的解;
(2)$\left\{\begin{array}{l}{y=2x-7①}\\{3x+y=8②}\end{array}\right.$,
把①代入②得:3x+2x-7=8,
解得:x=3,
把x=3代入①得:y=-1,
则方程组的解为$\left\{\begin{array}{l}{x=3}\\{y=-1}\end{array}\right.$.
点评 此题考查了解分式方程,以及解二元一次方程组,解方程组利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
18. 如图,把一块直角三角板的直角顶点放在直尺的一边上,如果∠1=22°,那么∠2的度数是( )
如图,把一块直角三角板的直角顶点放在直尺的一边上,如果∠1=22°,那么∠2的度数是( )
 如图,把一块直角三角板的直角顶点放在直尺的一边上,如果∠1=22°,那么∠2的度数是( )
如图,把一块直角三角板的直角顶点放在直尺的一边上,如果∠1=22°,那么∠2的度数是( )| A. | 22° | B. | 78° | C. | 68° | D. | 70° |
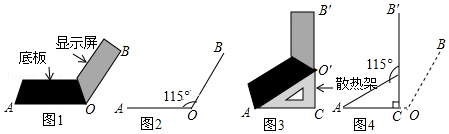
 如图,折叠宽度相等的长方形纸条,若∠1=64°,则∠2=52度.
如图,折叠宽度相等的长方形纸条,若∠1=64°,则∠2=52度. 如图,点O是线段AB和线段CD的中点,求证:△AOD≌△BOC.
如图,点O是线段AB和线段CD的中点,求证:△AOD≌△BOC.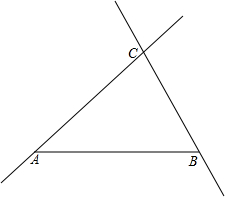 如图,公路AC、BC分别经过A、B两个工厂,现想修建一个货物中转站P,使它到两条公路AC、BC的距离相等,并且到A、B两个工厂的距离也相等.请你利用尺规确定货物中转站P的位置.(保留作图痕迹,不写作法)
如图,公路AC、BC分别经过A、B两个工厂,现想修建一个货物中转站P,使它到两条公路AC、BC的距离相等,并且到A、B两个工厂的距离也相等.请你利用尺规确定货物中转站P的位置.(保留作图痕迹,不写作法)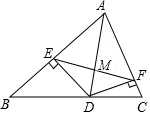 如图,AD为△ABC的角平分线,DE⊥AC于E,DF⊥AB于F,EF交AD于点M.
如图,AD为△ABC的角平分线,DE⊥AC于E,DF⊥AB于F,EF交AD于点M.