题目内容
 如图,△ABC三个顶点坐标分别为A(-2,3),B(-3,1),C(-1,1).
如图,△ABC三个顶点坐标分别为A(-2,3),B(-3,1),C(-1,1).(1)请画出△ABC关于y轴对称的△A1B1C1;
(2)以原点O为位似中心,将△A1B1C1放大为原来的2倍,得到△A2B2C2,请在第三象限内画出△A2B2C2,并求出S△A1B1C1:S△A2B2C2的值.
考点:作图-位似变换,作图-轴对称变换
专题:
分析:(1)根据关于y轴对称点的坐标性质求出对应点坐标,进而得出△A1B1C1;
(2)利用位似图形的性质得出对应点坐标,进而得出面积比.
(2)利用位似图形的性质得出对应点坐标,进而得出面积比.
解答: 解:(1)如图所示:△A1B1C1;
解:(1)如图所示:△A1B1C1;
(2)如图所示:△A2B2C2;
∵△A1B1C1放大为原来的2倍得到△A2B2C2,
∴△A1B1C1∽△A2B2C2,且相似比为
,
∴S△A1B1C1:S△A2B2C2=(
)2=
.
 解:(1)如图所示:△A1B1C1;
解:(1)如图所示:△A1B1C1;(2)如图所示:△A2B2C2;
∵△A1B1C1放大为原来的2倍得到△A2B2C2,
∴△A1B1C1∽△A2B2C2,且相似比为
| 1 |
| 2 |
∴S△A1B1C1:S△A2B2C2=(
| 1 |
| 2 |
| 1 |
| 4 |
点评:此题主要考查了位似变换以及轴对称变换和位似图形的性质,根据已知得出对应点位置是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 如图,这是一个由小立方块塔成的几何体的俯视图,小正方形中的数字表示该位置的小立方块的个数.请你画出它的主视图与左视图.
如图,这是一个由小立方块塔成的几何体的俯视图,小正方形中的数字表示该位置的小立方块的个数.请你画出它的主视图与左视图.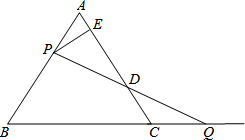 如图,△ABC是边长为12的等边三角形,P是AB上一动点,由A向B运动(与A、B点不重合),Q是BC延长线上一点,与点P同时以相同的速度由C向BC延长线方向运动(Q不与C点重合),过P作PE⊥AC于E,连接PQ交AC于D.
如图,△ABC是边长为12的等边三角形,P是AB上一动点,由A向B运动(与A、B点不重合),Q是BC延长线上一点,与点P同时以相同的速度由C向BC延长线方向运动(Q不与C点重合),过P作PE⊥AC于E,连接PQ交AC于D.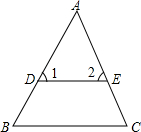 如图,在△ABC中,AB=AC,点D、E分别是AB、AC上的点,且DE∥BC,求证:△ADE是等腰三角形.
如图,在△ABC中,AB=AC,点D、E分别是AB、AC上的点,且DE∥BC,求证:△ADE是等腰三角形.