题目内容
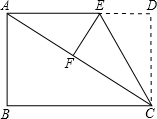 如图,在矩形ABCD中,AB=6,BC=8.将矩形ABCD沿CE折叠后,使点D恰好落在对角线AC上的点F处.
如图,在矩形ABCD中,AB=6,BC=8.将矩形ABCD沿CE折叠后,使点D恰好落在对角线AC上的点F处.(1)AC=
(2)EF的长为
考点:翻折变换(折叠问题)
专题:
分析:(1)在Rt△AC中,利用勾股定理列式计算即可得解;
(2)设EF=x,根据翻折的性质可得DE=EF=x,CF=CD=6,求出AF,然后在Rt△AEF中,利用勾股定理列出方程求解即可.
(2)设EF=x,根据翻折的性质可得DE=EF=x,CF=CD=6,求出AF,然后在Rt△AEF中,利用勾股定理列出方程求解即可.
解答:解:(1)在矩形ABCD中,∠B=90°,
∵AB=6,BC=8,
∴由勾股定理得,AC2=AB2+BC2=62+82=100,
∴AC=10;
(2)设EF=x,
∵矩形ABCD沿CE折叠后点D恰好落在对角线AC上的点F处,
∴DE=EF=x,CF=CD=6,
∵矩形ABCD中,AB=6,BC=8,
∴AD=BC=8,CD=AB=6,
∴AE=AD-DE=8-x,
AF=AC-CF=10-6=4,
在Rt△AEF中,AF2+EF2=AE2,
即42+x2=(8-x)2,
解得x=3,
故EF=3.
故答案为:10;3.
∵AB=6,BC=8,
∴由勾股定理得,AC2=AB2+BC2=62+82=100,
∴AC=10;
(2)设EF=x,
∵矩形ABCD沿CE折叠后点D恰好落在对角线AC上的点F处,
∴DE=EF=x,CF=CD=6,
∵矩形ABCD中,AB=6,BC=8,
∴AD=BC=8,CD=AB=6,
∴AE=AD-DE=8-x,
AF=AC-CF=10-6=4,
在Rt△AEF中,AF2+EF2=AE2,
即42+x2=(8-x)2,
解得x=3,
故EF=3.
故答案为:10;3.
点评:本题考查了翻折变换的性质,勾股定理,矩形的对边相等的性质,难点在于(2)利用勾股定理列出方程.

练习册系列答案
相关题目
二次函数y=x2-4x-1在-1≤x≤1范围内的最小值是( )
| A、-5 | B、-4 | C、-1 | D、4 |
 如图,圆心角∠AOB=100°,则圆周角∠ACB的度数是( )
如图,圆心角∠AOB=100°,则圆周角∠ACB的度数是( )| A、30° | B、45° |
| C、50° | D、60° |
已知一粒绿豆的质量约为0.000055千克,这个数用科学记数法表示为( )
| A、0.55×10-4 |
| B、5.5×10-5 |
| C、5.5×10-4 |
| D、55×10-6 |
如果一个多边形的内角和是外角和的5倍,那么这个多边形的边数是( )
| A、12 | B、11 | C、10 | D、9 |
 如图,△AEB≌△DFC,AE⊥CB,DF⊥BC,AE=DF,∠C=28°,则∠A=
如图,△AEB≌△DFC,AE⊥CB,DF⊥BC,AE=DF,∠C=28°,则∠A=