题目内容
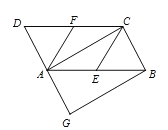
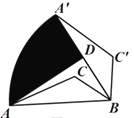
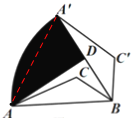
【题目】如图,在△ABC中,AB=4,若将△ABC绕点B顺时针旋转60°,点A的对应点为点A′,点C的对应点为点C′,点D为A′B的中点,连接AD.则点A的运动路径![]() 与线段AD、A′D围成的阴影部分面积是______.
与线段AD、A′D围成的阴影部分面积是______.
【答案】![]()
【解析】
连接AA′,由旋转的性质可得A′B=AB=4,∠ABA′=60°,即可证明△ABA′是等边三角形,根据点D是A′B的中点可知AD⊥A′B,利用∠ABD的三角函数值可求出BD、AD的长,根据S阴影=S扇形BAA′=S△ABD即可得答案.
连接AA′,
∵将△ABC绕点B顺时针旋转60°,AB=4,
∴A′B=AB=4,∠ABA′=60°,
∴△ABA′是等边三角形,
∵点D是A′B的中点,
∴AD⊥A′B,
∴BD=ABcos∠ABD=2,AD=ABsin∠ABD=2![]() ,
,
∴S阴影=S扇形BAA′=S△ABD=![]() -
-![]() ×2×2
×2×2![]() =
=![]() .
.
故答案为:![]()

练习册系列答案
相关题目
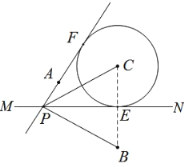
【题目】已知:点A、点B在直线![]() 的两侧.
的两侧.
(点A到直线![]() 的距离小于点B到直线
的距离小于点B到直线![]() 的距离).
的距离).
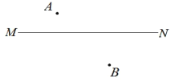
如图, (1)作点B关于直线 (2)以点C为圆心, (3)过点A作 (4)连接 |
|
根据以上作图过程及所作图形,下列四个结论中:
①![]() 是
是![]() 的切线; ②
的切线; ②![]() 平分
平分![]() ;
;
③![]() ; ④
; ④![]() .
.
所有正确结论的序号是___________________________.