Question

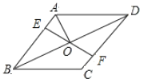
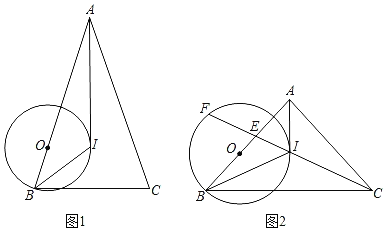
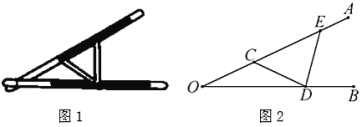
【题目】“三等分角”大约是在公元前五世纪由古希腊人提出来的.借助如图1所示的“三等分角仪”能三等分任一角.其抽象示意图如图2所示，由两根有槽的棒，组成，两根棒在点相连并可绕转动.点固定，，点，可在槽中滑动，

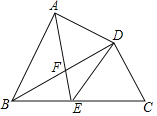
（1）求证：.

（2）若，

①求的度数；

②求点到的距离.

（参考数据：，，，，，）

Answer 1

【答案】（1）证明见解析；（2）①； ②点到的距离约为．

【解析】

（1）利用等边对等角结合三角形外角的性质即可证明；

（2）①作于点，根据等腰三角形 “三线合一”的性质求得OF的长，利用余弦函数的定义即可求得∠BOE的值，从而求得答案；

②作于点，利用正弦函数的定义即可求得答案．

（1）∵，

∴，

∵，

∴，

∴

；

（2）①过点作于点，如图：

∵，

∴，

∴，

∵，

∴，

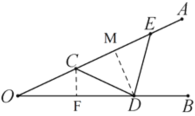
由（1）可知；

②过点作于点，

∵，

∴，

解得，

即点到的距离约为．